Presburger Arithmetic and Pseudo-Recursive Saturation
David Llewellyn-Jones
School of Mathematics and Statistics
The University of Birmingham
Edgbaston, Birmingham, B15 2TT, U.K.
Email
http://www.flypig.co.uk
August 2nd, 2001
The first half of this thesis looks at well known general properties of Presburger arithmetic, including quantifier elimination, types, compactness and homogeneity. It is accessible to the algebraist as well as the model theorist.
Let
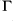
be a model of Presburger arithmetic. Define the residue map
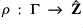
sending an element to the sequence of its remainders and the standard part
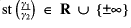
for
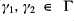
to be the supremum of the set
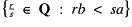
. Define a partitioning of our model by the equivalence relation
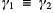
if and only if
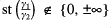
and let
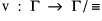
be the natural valuation.
We say that
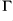
is pseudo-recursively saturated if: the inverse image of the residue map is dense in
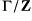
; for
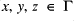
there exists
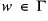
such that
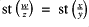
; and
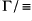
forms a dense linear order with least point
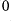
and no greatest point.
We prove that pseudo-recursive saturation implies homogeneity and give results in the opposite direction indicating an affinity between the two.
Our main result concerns the automorphism group,
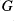
, of the countable pseudo-recursively saturated models of Presburger arithmetic, giving a correlation between the closed normal subgroups of
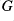
and sets of tuples of the standard parts of the model. We define
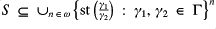
to be stQ-closed if: all subsets of
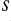
defined to be those tuples of a certain length form a group; if
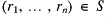
and
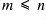
then
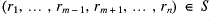
; and similarly if
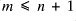
then there exists some
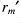
such that
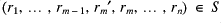
. We then have that
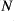
is a closed normal subgroup of
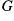
if and only if
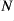
preserves some stQ-closed set
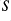
or
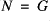
.
From this we are able to provide some results about the closed normal subgroups of
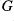
and to present a pair of Galois connections between closed normal subgroups of
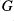
, stQ-closed subsets of the set of standard parts and equivalence relations on
.