Waste and recycling tracking
I try hard to minimise my environmental impact, but without being aware of the effect daily decisions have, it can be a challenge. Since moving to Finland I've become much more conscious of exactly how much energy I use, how much stuff I consume, the possessions I accumulate and how much waste all this activity produces.
Partly this is a result of me living in a one-person flat, and partly because since August 2019 I've been keeping an accurate record of how much waste I generate. Where I live in Tampere there are bins for six types of waste: paper, card, glass, metal, compost and general. Everything except the last of these is supposed to be recycled. Finland also has an exemplary network of financially-incentivised bottle and can returns. So each fortnight I find myself splitting waste into eight different categories. It's already effort, so taking weight measurements as well isn't a big deal.
This page covers the year up to my most recent readings. For older data, select on one of the links in the summary table.
| Year | Average daily output | Annual output | More info |
|---|---|---|---|
| 2019 | 339.53 g | 124 kg | 2019 graphs |
| 2020 | 154.98 g | 57 kg | 2020 graphs |
| 2021 | 119.88 g | 44 kg | 2021 graphs |
| 2022 | 122.93 g | 45 kg | 2022 graphs |
| All data | As of 01/2023: 155.81 g | As of 01/2023: 57 kg | Graphs of the complete dataset |
For comparison, in 2019 per capita annual household waste was 566 kg in Finland and 502 kg across the EU. See eurostat for other countries and years.
The following histocurve shows my daily waste output for this year based on data I collect each bin cycle roughly once per fortnight. The area under the graph represents my total waste output. Click on the graphs for larger versions.
Some brief points to note about the graph:
- Green categories are recycled by the council; general waste in red isn't recycled.
- This is output for a single person.
- Data points correspond to when I do the bins, roughtly fortnightly.
- For info about how the graphs are generated, see my Graphs of Waste posts on the topic.
- The script used to generate the graphs can be found on GitHub.
To view histograms showing the actual values recorded for each of the waste types, select one of the graphs below. Be aware that they all have different scales on the y-axis, so they're not visually comparable.
Waste
In previous years we've always tried to get a Christmas tree with roots. Our success rate in keeping it alive until the next Christmas currently stands at zero percent.
This year I went out of my way to care for our Christmas tree, carefully keeping the soil in its pot moist with daily watering, avoiding bumps and bashes, not overburdening the branches with crazy decorative figurines.
It's definitely fared better than any of our previous trees and today I dug a hole in the back garden and planted it solidly.
Here are the three stages of its life I've so far been involved with, from left-to-right: sitting in our living room right after we introduced it; with decorations ready for Christmas; and now transplanted to our back garden.
I'm no gardener and I don't rate its chances highly, but I'd love it to survive. Not only would it be wonderful to have a Norwegian Spruce living in our garden, but it would also feel like a real achievement to have a multi-year Christmas tree. I'm also counting this as one of the ecological acts needed to fulfil my New Year's Resolutions.
I'll report back later in the year on how the tree is doing. It feels like its success is now very much down to weather, nature and its will to survive. Maybe that's not the right way to look at these things, but that's why I'm not a gardener.
First there's the personal financial cost I incur from having to pony up a hundred quid or thereabouts each year. That's a good way to incentivize myself to reduce my carbon footprint in the future. Second there's the active process of interrogating my consumption: working through the calculations is a great way to focus the mind, confront the consequences of my personal decisions and think about what I could improve on in the future.
Last year it took until April for me to run the calculations and act on them. This year I've done much better. That's partly driven by my New Year's Resolution to make at least one ecological improvement per month during the year. Even though this isn't a new thing for me, when I made the resolution the intention was always to count this as one of the tasks. And so it is.
Here's the table that shows which carbon emissions came from which activities. I've included all previous years so that some trends can be captured. I should emphasise that this represents household emissions, so covers two people, both Joanna and me. For comparison average emissions for individuals in the UK is 5.40 tonnes (10.80 tonnes for two people).
| Source | CO2, 2019 (t) | CO2, 2020 (t) | CO2, 2021 (t) | CO2, 2022 (t) | CO2, 2023 (t) |
|---|---|---|---|---|---|
| Electricity | 0.50 | 0.40 | 0.59 | 1.14 | 1.66 |
| Natural gas | 1.18 | 1.26 | 1.66 | 0.81 | -0.25 |
| Flights | 5.76 | 2.26 | 1.90 | 5.34 | 1.32 |
| Car | 1.45 | 0.39 | 0.39 | 1.01 | 1.00 |
| Bus | 0.00 | 0.01 | 0.02 | 0.01 | 0.31 |
| National rail | 0.08 | 0.01 | 0.02 | 0.00 | 0.70 |
| International rail | 0.02 | 0.01 | 0.00 | 0.04 | 0.01 |
| Taxi | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Food and drink | 1.69 | 1.11 | 1.05 | 1.35 | 1.07 |
| Pharmaceuticals | 0.26 | 0.32 | 0.31 | 0.06 | 0.13 |
| Clothing | 0.03 | 0.06 | 0.06 | 0.12 | 0.23 |
| Paper-based products | 0.34 | 0.15 | 0.14 | 0.37 | 0.38 |
| Computer usage | 1.30 | 1.48 | 0.75 | 0.93 | 0.23 |
| Electrical | 0.12 | 0.29 | 0.19 | 0.03 | 0.01 |
| Non-fuel car | 0.00 | 0.10 | 0.00 | 0.12 | 0.92 |
| Manufactured goods | 0.50 | 0.03 | 0.03 | 0.05 | 0.11 |
| Hotels, restaurants | 0.51 | 0.16 | 0.15 | 0.10 | 1.21 |
| Telecoms | 0.15 | 0.05 | 0.04 | 0.03 | 0.05 |
| Finance | 0.24 | 0.24 | 0.22 | 0.04 | 0.02 |
| Insurance | 0.19 | 0.11 | 0.10 | 0.04 | 0.04 |
| Education | 0.05 | 0.00 | 0.04 | 0.01 | 0.00 |
| Recreation | 0.09 | 0.06 | 0.05 | 0.03 | 0.06 |
| Total | 14.47 | 8.50 | 7.73 | 11.65 | 9.25 |
The headline result is that our total carbon emissions have been reduced compared to last year. That's mostly driven by a large decrease in the number of flights, from twenty in 2022 to just four last year. Twenty flights is a large number, a consequence of living in Finland. This year I moved back to the UK in February. That meant some flights to tidy up my life in Finland, but I've not flown again since then. In 2024 I'm hoping to push that down to zero flights.
Reduced flights was partly offset by increased train and bus travel, largely due to my weekly commute between Cambridge and London for work. I took the journey 88 times, giving me a massive total distance travelled of 19 638 km by national rail. Thankfully trains are also far more carbon efficient than planes, so while distance travelled only reduced by a factor of 1.5, carbon emissions reduced by a factor of 5.75.
One potentially confusing thing about the numbers is that natural gas usage is a negative figure. We switched from a gas boiler to a heat pump, with the result that our gas usage tumbled. But of course it wasn't negative! The negative value is due to our power company overestimating our gas usage as a result of our heating change. The overestimate was included in the figures for last year and this negative figure redresses that.
The following table gives more detail about the numbers used to perform the calculations. After pulling these together I then fed them into Carbon Footprint Ltd's carbon calculator as I have in previous years to generate the results.
| Source | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|
| Electricity | 1 794 kWh | 1 427 kWh | 3 009 kWh | 4 101 kWh | 5 975 kWh |
| Natural gas | 6 433 kWh | 6 869 kWh | 9 089 kWh | 4 439 kWh | -1 362 kWh |
| Flights |
36 580 km 20 flights |
14 632 km 8 flights |
25 542 km 14 flights |
36 042 km 20 flights |
7 233 km 4 flights |
| Car | 11 910 km | 2 000 km | 3 219 km | 8 458 km | 8 369 km |
| Bus | 1 930 km | 40 km | 168 km | 133 km | 3 080 km |
| National rail | 5 630 km | 400 km | 676 km | 0 km | 19 638 km |
| International rail | 64 km | 1 368 km | 513 km | 8 684 km | 2 322 km |
| Taxi | 64 km | 37 km | 100 km | 100 km | 100 km |
| Tube | 0 km | 0 km | 0 km | 0 km | 100 km |
As in previous years I've used the UN Framework Convention on Climate Change to offset my carbon output. The money will go to pay for improved cooking stoves in Malawi, a scheme managed by Ripple Africa.
It's now Sunday 4th June, nearly six months after I moved from Finland to the UK and finished collecting data, and high time I put pen to paper... fingers to keyboard... to write up the results. There's going to be quite a lot to look at here, so I've split it into three sections: my waste data output; my consumption data input; and how they relate to one another.
Waste Data Output
Let's start with my outputs. I collected data about my rubbish from 18th August 2019 through to 1st January 2023, nearly three and a half years. You can read all about the results from earlier years on my waste pages.
What of 2022? As with previous years there are peaks and troughs that go alongside my activities. There's a big spike around Christmas when Joanna visited and we had two whole people living in my flat (we don't see the same spike in 2021 because that year I spent Christmas with Joanna in the UK). There's a trough around August when Joanna and I went on holiday. Similar holiday troughs — at slightly different times of year — can be seen in 2020 and 2021.
It's hard to get an overall picture from this temporal view, so perhaps the overall averages for the different categories are more insightful. These are shown on the right hand side of the graph. It's also interesting to compare them against previous years. Here's the same information collated into a couple of graphs.
On the left hand side we can see the weight of waste output for each category. This is the average daily output for the stated year. As you can see, I worked quite hard to reduce my waste output year-on-year, cutting it by around half in 2020 and then by nearly a quarter again in 2021. That seems to have been my limit though: my 2022 level is just marginally higher than in 2021.
To understand what changed, it's helpful to look at the graphs in terms of proportions rather than absolute values. The right hand graph shows each of the outputs as a proportion of the total year's output. What we can see is that from 2019 to 2021 I greatly reduced my glass and metal output. Looking at both graphs, we can see that I also reduced my paper and compost output quite considerably, but not as an overall proportion.
In contrast, both the proportions and absolute values for 2021 and 2022 are very similar.
None of this is a huge surprise to me: I worked really hard to reduce my glass, metal and paper waste. I cut glass bottles and metal cans out of my shop almost entirely, switching them to plastic bottles, cardboard cartons and cardboard containers instead. You can read more about my reasoning for doing this in an earlier post. I cut down my paper waste output by putting a sing reading 'Ei mainoksia kiitos!' on my door (simple things) and by restructuring my magazine and postal subscriptions.
The following table gives the values for each of the categories in full. This is my average daily waste output measured in grammes.
| Year | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|
| General | 45.16 | 28.33 | 28.26 | 29.28 |
| Plastic | 6.65 | 11.27 | 9.52 | 9.97 |
| Compost | 94.84 | 43.51 | 31.11 | 27.85 |
| Returnables | 8.70 | 5.99 | 6.36 | 5.33 |
| Metal | 6.86 | 0.32 | 0.16 | 0.49 |
| Glass | 77.24 | 13.29 | 1.81 | 0.95 |
| Card | 35.27 | 27.44 | 20.93 | 23.89 |
| Paper | 64.82 | 24.83 | 21.73 | 25.18 |
| Total | 339.53 | 154.98 | 119.88 | 122.93 |
These values are rather small and hard to handle, so it can help to understand what these numbers mean on an annual basis. The following table shows the same values given in kilograms and multiplied up by a factor of 365.25. These represent the amount of waste for each category that I generated over the period of a year measured in kilogrammes.
| Year | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|
| General | 16.50 | 10.35 | 10.32 | 10.70 |
| Plastic | 2.43 | 4.12 | 3.48 | 3.64 |
| Compost | 34.64 | 15.89 | 11.36 | 10.17 |
| Returnables | 3.18 | 2.19 | 2.32 | 1.95 |
| Metal | 2.50 | 0.12 | 0.06 | 0.18 |
| Glass | 28.21 | 4.85 | 0.66 | 0.35 |
| Card | 12.88 | 10.02 | 7.64 | 8.73 |
| Paper | 23.67 | 9.07 | 7.94 | 9.20 |
| Total | 124.01 | 56.61 | 43.78 | 44.90 |
Consumption Data Input
Now let's look at my 2022 consumption data. The following graph shows what I bought in terms of weight. The categories were chosen by going through each item and selecting one of the existing categories if it fit, or creating a new one otherwise. The software I used for doing this is in the repository on GitHub.
It's interesting that there's so much variation through the year. Often this is driven by specific categories. I bought especially large quantities of soft drink in March, April and November, probably because of the weather. There are a few periods where my purchasing dropped to zero, because I was travelling away from home. Otherwise the cycle seems to be largely based on a three-week shopping period.
This is actually contrary to what I would have expected. I had thought my shopping cycle was roughly weekly, with smaller more frequent shopping trips for essentials (such as bread). But the graph tells me that in practice my shopping increased every third week or so. If I'd known this I might have organised things more intentionally.
Weight and costs are different things of course. The following graph shows the same purchases in terms of their cost in Euros, rather than their weight in grams. Although you can still see the same three-week shopping cycle, things do shift quite substantially. Drinks and 'other food' are costly (the former is also heavy, but the latter not). During the winter months 'other non-food' becomes a significant cost for me. That's probably Christmas presents.
Let's summaries all the results in terms of annual daily averages for the year. The following graph shows the details for all of the data I collected: number of items, weight of items and cost of items.
From this we can see that I'm buying over a kilogram of 'stuff' per day. That's more than I would have expected. The cost of all this stuff is averaging out to €12.20 per day. That's the cost of consumables it takes to run a human. That doesn't include rent, bills, transport, furniture: it's essentially just groceries. Again, that's more than I was expecting.
At this point we're already in a position to compare some of these inputs against outputs. For example, my overall daily input weight of 1171 g per day is getting converted into an output weight of 122.93 g per day. There's a big difference between the two, so where's all that extra weight going? Well, mostly down the toilet and sink I'd imagine.
In the next section we'll break all this down further and do a more careful comparison between inputs and outputs.
Garbage In, Garbage Out
It's interesting to consider how much waste I produce and how much it's all costing me. But by collecting this data, what I really hoped to discover was some connection between the two. The majority of things I throw away are at some time prior to that something I've bought.
In order to understand this relationship better the first step needed is to recategorise my consumption data to match those of my waste data. Given I catalogued exactly what I bought on each occasion, the underlying consumption data I've collected is far more detailed than the waste data I collected, so it makes sense to map the consumption data onto the waste data rather than vice versa.
Here's the graph showing my consumption graphed across the year, measured by weight and split across the eight waste categories. You'll notice that the total weight matches exactly with the graph above showing the data more finely categorised. However the individual strata that make up the total are quite different.
We can also render the cost graph using the same categories. Again, the total cost matches that of our earlier cost graph, but the individual strata that make it up are quite different. This is as we might expect.
Assigning a waste category to each of my purchases turns out to be quite challenging. Consider a box of tea. Should this be categorised as card for the box the tea comes in, or compost for the tea-leaves that are thrown away after brewing? My solution was to give each item only a single category, but to pick the one that disproportionately affects the waste that's thrown away. This involved some judgement calls that weren't always as clear cut as I'd have liked.
The following graph shows the annual summary for the data stratified into waste categories.
Comparing this against the waste summary graphs from earlier, there's obviously a big discrepancy between the weight of inputs and the weight of outputs: there's a roughly ten fold difference. But as we discussed earlier, this isn't unexpected. The proportions don't match up either: general waste makes up a larger proportion of my consumption input than it does my waste output, while the reverse is true for paper.
There are multiple reasons why this might be the case. Miscategorisation is one, but just as likely is that the weight ratios of inputs versus outputs aren't directly comparable. For example, a carton of orange juice is much heavier than a box of doughnuts, but they'll both end up generating a similar mass of cardboard waste. Once again, this highlights how much of an inexact process this all is.
Nevertheless it would be interesting to see if we can track inputs and see how long it takes for them to become outputs. If we can find this, it would provide an idea of how long it takes items within a given category to move from bought to binned. To estimate this we take each of the categories and compare the mean squared error of the consumption and waste data summed over time. We calculate the errors for different offsets between the waste data and the consumption data and compare them. The offset represents how long it takes for something to end up in the bin after purchase.
By minimising the mean square error over the offest we can find the offset that gives the best fit between the two graphs.
Given the ten-fold discrepancy between input weights and output weights, we normalise the data by scaling it so that both inputs and outputs sum to the same value across the year. The following figure shows the errors for each of the categories at different offsets. What we're interested in is the minimum point for each of the lines.
As you can see, in many of the cases the graph drops down to a single local minimum and then goes up again. This is an ideal situation as it gives us a clear candidate for generating the smallest error.
The remaining graphs at the end of this post show the normalised consumption and waste graphs for each of the categories, with the optimal offset applied.
As we can see, there's quite a range, and in some cases (paper, glass) the data is dominated by a few large purchases. In other cases we see a far noisier-looking graph for consumption as compared to waste. This is an artefact of my shopping patterns: while I recorded purchases throughout the week, I tended to only take waste readings fortnightly.
The table below lists the offsets that result in the smallest average mean square error for each of the categories.
| Category | Min mean square error | Offset (days) |
| general | 8.700 × 10-6 | 1 |
| plastic | 1.075 × 10-5 | 4 |
| compost | 9.964 × 10-6 | 0 |
| returnables | 1.729 × 10-5 | 1 |
| metal | 1.137 × 10-4 | 0 |
| glass | 4.296 × 10-5 | 9 |
| card | 1.483 × 10-5 | 10 |
| paper | 1.672 × 10-5 | 15 |
| all | 9.008 × 10-6 | 4 |
The error values don't tell us much since they can't be compared across categories (the values depend on the normalisation scaling which are different for each category). The offsets are the more interesting values. These range between zero days for metal and compost, and fifteen days for paper.
Given the small quantity that went through my household across the year (a total of 180 g), the result for metal isn't so suprising. The result for compost is less clear: there was a relatively consistent flow of compost throughout the year, which could explain the lack of offset. We can see both of these situations in the detailed graphs for metal and compost at the end of this post.
At the other end of the spectrum, paper has a turnaround rate of fourteen days, while glass and card have turnarounds of nine and ten days respectively. The remaining cases are less than a week.
If these are correct, they're interesting results. And they don't seem implausible. However in practice the data is so noisy, and I had to make so many assumptions while processing it, that I wouldn't put much stock in these results.
For all of my inputs and outputs combined the expected turnaround is four days. That's not implausible either, but again, I wouldn't give it much credence. To get a more accurate result, I'd had to have matched inputs with outputs exactly. I collected enough data on my consumption habits for this, but not on my waste-generating habits. I'd have needed to record each of the items in my bins and matched them to the items I bought previously. It's not implausible to imagine I could have done this, but sadly I didn't realise that these were data I'd really need for this analysis.
Summary
What can we conclude from all of this? The most actionable point I get from this is that my efforts to reduce my waste output by cutting out glass and metal, and cutting down on newspapers and magazines, were successful. This is a lesson I take forward.
My three week shopping cycle is also something I could potentially benefit from knowing. I should be planning my menus and performing one main shop every three weeks, with smaller top-ups from the local market in between.
Finally, matching consumed inputs with waste outputs turned out to be more challenging than I was expecting, to the extent that it's not clear how much I really achieved from recording everything I purchased in quite such detail.
Nevertheless I feel it was a worthwhile experience: I definitely gained something intangible from the process that isn't reflected in the analysis of the data. I'll continue to estimate my CO2 output and try to reduce the amount of waste I generate on a daily basis. This is the real win: I'm much more aware of what I buy and throw away, and for me, reducing this waste is a crucial aspect of limiting my negative impact on the wider environment.
With that in mind, I've spent the last couple of weekends calculating my carbon footprint for 2022. The act of doing this has in itself been a useful exercise, helping highlight where I've been succeeding, and where I've been failing. But the final objective is to allow me to offset my carbon output, which as last year, I've done by contributing to the Ripple Africa initiative providing lower carbon cooking stoves in Malawi.
Here are the results for 2022, with comparison to earlier years and compiled once again using Carbon Footprint Ltd's carbon calculator. These results are for both Joanna and me, so I consider them to be outputs equivalent to a two-person household (even though we were actually living in different places throughout 2022).
| Source | CO2 output 2019 (t) | CO2 output 2020 (t) | CO2 output 2021 (t) | CO2 output 2022 (t) |
|---|---|---|---|---|
| Electricity | 0.50 | 0.40 | 0.59 | 1.14 |
| Natural gas | 1.18 | 1.26 | 1.66 | 0.81 |
| Flights | 5.76 | 2.26 | 1.90 | 5.34 |
| Car | 1.45 | 0.39 | 0.39 | 1.01 |
| Bus | 0.00 | 0.01 | 0.02 | 0.01 |
| National rail | 0.08 | 0.01 | 0.02 | 0.00 |
| International rail | 0.02 | 0.01 | 0.00 | 0.04 |
| Taxi | 0.01 | 0.01 | 0.01 | 0.01 |
| Food and drink | 1.69 | 1.11 | 1.05 | 1.35 |
| Pharmaceuticals | 0.26 | 0.32 | 0.31 | 0.06 |
| Clothing | 0.03 | 0.06 | 0.06 | 0.12 |
| Paper-based products | 0.34 | 0.15 | 0.14 | 0.37 |
| Computer usage | 1.30 | 1.48 | 0.75 | 0.93 |
| Electrical | 0.12 | 0.29 | 0.19 | 0.03 |
| Non-fuel car | 0.00 | 0.10 | 0.00 | 0.12 |
| Manufactured goods | 0.50 | 0.03 | 0.03 | 0.05 |
| Hotels, restaurants | 0.51 | 0.16 | 0.15 | 0.10 |
| Telecoms | 0.15 | 0.05 | 0.04 | 0.03 |
| Finance | 0.24 | 0.24 | 0.22 | 0.04 |
| Insurance | 0.19 | 0.11 | 0.10 | 0.04 |
| Education | 0.05 | 0.00 | 0.04 | 0.01 |
| Recreation | 0.09 | 0.06 | 0.05 | 0.03 |
| Total | 14.47 | 8.50 | 7.73 | 11.65 |
The first thing to note is that there's been abig increase compared to my carbon output in 2021 and 2022. The main contributor to this has been carbon emissions due to flying, and the factor with the biggest impact on this has been the pandemic. For all of the years shown here I was living in Tampere, Finland while Joanna was living in Cambridge, UK. Travelling between the two by train (and boat) takes a full four days, compared to a day's travel by plane (and car/train). During the pandemic our ability to travel was naturally curtailed. It's worth looking into the associated numbers here in more detail.
| Source | Details for 2019 | Details for 2020 | Details for 2021 | Details for 2022 |
|---|---|---|---|---|
| Electricity | 1 794 kWh | 1 427 kWh | 3 009 kWh | 4 101 kWh |
| Natural gas | 6 433 kWh | 6 869 kWh | 9 089 kWh | 4 439 kWh |
| Flights | 36 580 km (20 flights) | 14 632 km (8 flights) | 25 542 km (14 flights) | 36 042 km (20 flights) |
| Car | 11 910 km | 2 000 km | 3 219 km | 8 458 km |
| Bus | 1 930 km | 40 km | 168 km | 133 km |
| National rail | 5 630 km | 400 km | 676 km | 0 km |
| International rail | 64 km | 1 368 km | 513 km | 8 684 km |
| Taxi | 64 km | 37 km | 100 km | 100 km |
I moved back to the UK at the start of 2023 and now that Joanna and I are living together again, I'd expect our plane travel to reduce to just a handful of trips a year (our aim has to be zero).
My flat in Tampere was incredibly well insulated, but nevertheless still required heating and lighting. Now that I'm back in the UK and no longer renting a flat in Tampere, our overall heating requirements should reduce in 2023. It's also worth noting that our natural gas usage decreased in 2022, while our electricity usage increased. This will be due to the fact we installed a heat pump in February of 2022, so that our heating is now fully renewable rather than gas. For 2023 the balance should shift further.
Our car usage increased again back to something closer to pre-pandemic levels. This is due to Joanna travelling to work again (I had no access to a car in Finland). Our International Rail travel also increased due to two factors: partly because I'm now including all long-distance rail under the category, and partly because we travelled by Eurostar on a couple of occasions.
From the numbers it's clear Joanna and I travelled our longest distances by plane, but the numbers also highlight another important consideration. Each kilometre travelled by plane resulted in 148 g of CO2 (this includes a radiative forcing factor of 1.891), compared to 119 g for car travel and 75 g for bus travel. But according to these numbers train travel generated only 5 g of CO2 per kilometre. That's a huge differential.
Looking at the overall emissions compared to last year I was initially dispirited, but after more careful consideration I'm actually quite encouraged. Joanna and I reduced our carbon output considerably since 2019, which is a fairer point of comparison given the effects of the pandemic in 2020 and 2021. Our move from gas to heat-pump heating is shown positively in the numbers and will have an even bigger impact in 2023 when it covers the whole year. With me moving back to the UK we will be servicing only one household rather than two, and our reliance on flying will decrease, addressing the single largest contributor to our carbon footprint.
For comparison the average carbon footprint in the European Union is 6.8 tonnes, while world wide it's 4.79 tonnes. Split between Joanna and me, our individual footprints average out at 5.825 tonnes. That's clearly too high, but hopefully things are looking more promising for 2023.
In the meantime, I've once again used the UN Framework Convention on Climate Change to offset our emissions for 2022.
The site doesn't take payment itself, instead it hooks you up with the projects so you can pay directly. Unfortunately I experienced some difficulty trying to pay my preferred project at the time, and ultimately had to give up on it.
It's taken a while for me to catch up to it again, but I finally got around to trying with a different project. Happily I had more success on this second attempt, and our emissions are now being offset by RIPPLE Africa by providing lower carbon cooking stoves in Nkhata Bay District, Malawi.
It turns out that 2021 was a good year for me environmentally, or that it at least looks that way on paper. Hemmed in by the pandemic and forced to reduce flying, it wasn't hard to do less this year. On top of that 2021 made my third year of collecting waste data, which — even unconsciously — has trained me into throwing less stuff away.
So let's start with my 2021 household carbon footprint. According to the Carbon Footprint Calculator, in 2021 Joanna and I contributed a combined total of 7.73 tonnes of CO2 to the atmosphere. That's a lot of CO2, but our output is at least following a downward trend. In 2019 we contributed 14.47 tonnes and in 2020 it was 8.50 tonnes. The following table summarises where all that gas came from.
| Source | Details for 2021 | CO2 output 2019 (t) | CO2 output 2020 (t) | CO2 output 2021 (t) |
|---|---|---|---|---|
| Electricity | 3 009 kWh | 0.50 | 0.40 | 0.59 |
| Natural gas | 9 089 kWh | 1.18 | 1.26 | 1.66 |
| Flights | 3 HEL-LHR, 4 TMP-STA | 5.76 | 2.26 | 1.90 |
| Car | 3 219 km | 1.45 | 0.39 | 0.39 |
| Bus | 168 km | 0.00 | 0.01 | 0.02 |
| National rail | 676 km | 0.08 | 0.01 | 0.02 |
| International rail | 513 km | 0.02 | 0.01 | 0.00 |
| Taxi | 100 km | 0.01 | 0.01 | 0.01 |
| Food and drink | 1.69 | 1.11 | 1.05 | |
| Pharmaceuticals | 0.26 | 0.32 | 0.31 | |
| Clothing | 0.03 | 0.06 | 0.06 | |
| Paper-based products | 0.34 | 0.15 | 0.14 | |
| Computer usage | 1.30 | 1.48 | 0.75 | |
| Electrical | 0.12 | 0.29 | 0.19 | |
| Non-fuel car | 0.00 | 0.10 | 0.00 | |
| Manufactured goods | 0.50 | 0.03 | 0.03 | |
| Hotels, restaurants | 0.51 | 0.16 | 0.15 | |
| Telecoms | 0.15 | 0.05 | 0.04 | |
| Finance | 0.24 | 0.24 | 0.22 | |
| Insurance | 0.19 | 0.11 | 0.10 | |
| Education | 0.05 | 0.00 | 0.04 | |
| Recreation | 0.09 | 0.06 | 0.05 | |
| Total | 14.47 | 8.50 | 7.73 |
The main reasons for the reduction compared to 2020 were fewer flights, and fewer computer purchases (I purchased precisely one less laptop than the one I purchased in 2020). Laptops, it turns out, are surprisingly carbon-intensive to make.
So those reductions are benefits, but I'm not sure they're benefits we'll be able to maintain over time. In early 2022 we've arranged to have a heat pump installed to replace our gas central heating. This is a big change, with the main aim to reduce that 9 089 kWh of natural gas usage in the table above. Gas is clean to burn, but as a non-renewable fossil fuel it's especially problematic, with no easily switchable environmentally-friendly alternative. Hopefully a heat pump will reduce our overall power usage, not just our non-renewable usage.
Our numbers equate to an average of 3.87 tonnes of CO2 per person in 2021. That compares favourably to the UK average of 5.4 tonnes, an EU average of 6.4 tonnes and a world average of 4.8 tonnes according to the World Bank.
How about waste output? My average waste output for 2021 was 114.69 g/day. You can see how this came about, and how it was split across different types of waste, in the graph below.
This average is equivalent to a total waste output of 42 kg for the year. In theory everything except the General waste shown in the graph was recycled. The total is also a reduction on previous years, comparing to 57 kg of output in 2020 and 118 kg in 2019. These number are slightly lower than the actual amount. For example this year I've spent around six weeks in the UK, during which I'm not able to collect waste output data.
This all looks quite positive, but I'm becoming increasingly aware that waste output is a volatile metric. For example, if at some point I have to replace a piece of furniture, my waste output will go through the roof for the year. This does honestly motivate me to try to fix things rather than throw them away, but it's also a source of angst, knowing that it'll happen eventually.
According to eurostate, average per capita municipal waste output across the EU was 505 kg per person, with the average in Finland being slightly higher at 596 kg. Compared to this, my 42 kg of output looks pretty good. Still, I'm supposing that at least some of that 505 kg was made up of chairs.
So in summary I'm happy that Joanna's and my CO2 output was down on 2020, as was my waste output. We both trod a bit more lightly, even if it's not yet light enough. We've not quite reached that fully circular economy. The main driving factor for the reduction seems to have been the pandemic, so it will at least be interesting to see what happens next year.
I attribute this improvement squarely to the act of measuring my data each fortnight. The process has made me far more aware, not just about how much waste I produce, but also the sorts of products that generate more or less waste.
For example, glass is really heavy and it became clear quite early on that it was contributing significantly to the weight of waste I was producing. This motivated me to look into it more deeply, which ultimately resulted in me almost completely eradicating glass from my daily usage.
As a result of this and other changes, my daily usage has gone down from 322.80 g/day in 2019 to 154.98 g/day in 2020, and now in 2021 I'm currently averaging 123.34 g/day. Admittedly my average this year is likely to increase during the winter (and Christmas especially) but my aim is to keep it at least as low as my 2020 average.
One of the downsides to accumulating all this data is that the graphs I've been posting here have become increasingly hard to read. Placing all of the data onto a single graph has become unsustainable, so over the last week I've been updating my graph-generating scripts to make them more flexible. As a result, I'm now going to only show data for the current year on the main waste page. The data for previous years can still be viewed on the pages for 2019 and 2020, and I'll add new pages as the years tick forwards.
I've also created a new page showing the complete data set. These "all-data" graphs are plotted wider now, and while this makes it easier to read the individual entries, it also makes them impractically long and thin. The "fixed in time" preview below already gives an idea of the problem, but the graphs will only get wider, and the issue more accuate, over time. So they're really only going to be of interest for the masochistic.
While the full-data graph is interesting by virtue of its absurdity, splitting the graph up into annual chunks turns out to be the more interesting case. In particular, because I take readings when I take out the rubbish, these rarely actually fall on the first or last day of the year. So, how to split the readings across the year boundaries?
The solution I've came up with is to scale the readings at each end of the year in proportion to how much of the period falls into the year in question. For example, here are the actual readings I took over the 2020-2021 year boundary.
| Date | Paper | Card | Glass | Metal | Returnables | Composts | Plastic | General |
|---|---|---|---|---|---|---|---|---|
| 12/12/2020 | 57 | 515 | 0 | 0 | 0 | 449 | 107 | 322 |
| 14/3/2021 | 641 | 225 | 0 | 0 | 93 | 443 | 88 | 473 |
This covers an unusually long period of time because I was stuck in the UK for January, February and most of March due to Covid travel restrictions. But this is also convenient for making a more exaggerated example. So the period between 12th December and 14th March contains a total of 92 days. That splits into the two periods "12th December - 31st December" and "1st January - 14th March", which contain 20 and 72 days respectively. The proportion of time for each of these periods is therefore 20 / 92 = 21.74% that falls into 2020 and 72 / 92 = 78.26% that falls into 2021.
To manage the data split across the year, we therefore have to scale it appropriately. Each entry represents the end of a period, so the 12th December data falls entirely within 2020. The 14th March data represents the period that's split across both years. We can therefore scale this entry and turn it into two separate entries like this, scaling each of the data points based on the proportions calculated above.
| Date | Paper | Card | Glass | Metal | Returnables | Composts | Plastic | General |
|---|---|---|---|---|---|---|---|---|
| 31/12/2020 | 139.35 | 48.91 | 0 | 0 | 20.22 | 96.30 | 19.13 | 102.83 |
| 14/3/2021 | 501.65 | 176.09 | 0 | 0 | 72.78 | 346.70 | 68.87 | 370.17 |
To get the correct picture this has to be done at both ends of the year being plotted.
Managing the data this way makes some obvious assumptions which may not necessarily be true (it assumes I generate waste uniformly across the time period, which is obviously not the case). However it has several nice properties. The annual histograms get drawn in a way that broadly speaking matches up across the year boundary; and the annual averages also match up correctly. At least, it seems to me to be the most honest way to tackle the issue when apportioning the data across year boundaries.
Check back to my waste page over time to see how I'm getting on with keping my waste output down (or not), and whether I'm able to hit my 2021 target.
So, whilst reducing production is always the best goal, it's still necessary to think about what to do with the remaining output. A quick search on the Internet will reveal a massive choice of carbon offsetting schemes, and when I looked into it last year I was basically overwhelmed. There's plenty of advice (is it good advice?) to suggest which schemes to go for. There's plenty of advice (is it good advice?) telling you that it's a pointless exercise. I don't know whether it's worth it or not, but at worst it's an opportunity to be scammed, while at best it might actually be doing some good. That pushes the risk-reward balance over into the positive for me.
Last year I ended up using Karbonaut to offset my output. The words on the website made it look legitimate with claims to be contributing to "Gold Standard" projects. But in practice I wasn't going on much. Well, Karbonaut is now "closed", which isn't a good sign. Not that I'm suggesting it isn't legitimate, but at least it meant this year I had to start my search all over again.
So, it was with some relief and happiness that I discovered that the UN runs a centralised carbon offsetting platform as part of the United Nations Framework Convention on Climate Change. You don't have to be a government or company to use it, any individual can just rock up at offset.climateneutralnow.org and use it to contribute to a carbon offsetting project. The money goes directly to the project you choose and there's plenty of in-depth documentation about every project to help decide which to go for.
At the end of the process you even get a convincing looking Voluntary Cancellation Certificate. If you're thinking of offsetting your carbon footprint, I strongly recommend it.
We were determined to improve on this in 2020 and gave ourselves some targets to hit. Then of course 2020 turned out to be an atypical year, to put it mildly. We both spent the majority of the year working from home. For six months we were in separate countries unable to travel to see each other. And while this was bad in many ways, it did at least have an impressive effect on our carbon footprint.
With our ability to travel seriously curtailed, the numbers look very different for 2020. Here's the complete breakdown, including the respective values for 2019 and the goals that we set ourselves back in April.
| Source | Details for 2020 | CO2 output 2019 (t) | Goal for 2020 (t) | CO2 output 2020 (t) |
|---|---|---|---|---|
| Electricity | 1 427 kWh | 0.50 | 0.25 | 0.40 |
| Natural gas | 6 869 kWh | 1.18 | 1.18 | 1.26 |
| Flights | 4 return HEL-LON | 5.76 | 3.46 | 2.26 |
| Car | 2 000 km | 1.45 | 0.97 | 0.39 |
| Bus | 40 km | 0.00 | 0.00 | 0.01 |
| National rail | 400 km | 0.08 | 0.16 | 0.01 |
| International rail | 1 368 km | 0.02 | 0.04 | 0.01 |
| Taxi | 37 km | 0.01 | 0.02 | 0.01 |
| Food and drink | 1.69 | 1.69 | 1.11 | |
| Pharmaceuticals | 0.26 | 0.26 | 0.32 | |
| Clothing | 0.03 | 0.03 | 0.06 | |
| Paper-based products | 0.34 | 0.34 | 0.15 | |
| Computer usage | 1.30 | 1.30 | 1.48 | |
| Electrical | 0.12 | 0.12 | 0.29 | |
| Non-fuel car | 0.00 | 0.00 | 0.10 | |
| Manufactured goods | 0.50 | 0.10 | 0.03 | |
| Hotels, restaurants | 0.51 | 0.51 | 0.16 | |
| Telecoms | 0.15 | 0.15 | 0.05 | |
| Finance | 0.24 | 0.24 | 0.24 | |
| Insurance | 0.19 | 0.19 | 0.11 | |
| Education | 0.05 | 0.05 | 0.00 | |
| Recreation | 0.09 | 0.09 | 0.06 | |
| Total | 14.47 | 11.14 | 8.50 |
In some areas we didn't hit our targets, but when it comes to travel we obliterated them. The final result is a combined carbon footprint of 8.5 tonnes of CO2, or 4.25 tonnes each. That's really quite good, taking us well below the UK (6.5 tonnes) and EU (6.4 tonnes) averages, and even taking us below the worldwide average of 5 tonnes.
If 2020 had been a normal year we clearly would have struggled to keep our footprint so low. But it's all the same to the environment and so I'm glad for the improvement.
Turning to the future, the real question will be whether we can sustain this same low level in 2021. Given the uncertainty of what lies ahead and the peculiar circumstances we experienced last year, it doesn't seem sensible to try to set a lower target, but rather to simply aim to match what we did in 2020 and see how we get on with that.
If you're interested to calculate your own carbon footprint, I can recommend the Carbon Footprint Calculator I used to compile the values here. It really made the process surprisingly painless.
The rented flat where I live comes with a dishwasher, but I've never actually used it. The main reason is that I don't have enough crockery to fill it, but maybe I should? I've been told in discussion, and also by advertisements, that using a dishwasher is more ecological than washing up by hand. This always seemed a bit implausible to me, but maybe it's true?
Let's find out.
First of all, how much energy is needed to do a batch of washing up? This depends on what you do, but my washing up regime is pretty consistent: I fill the sink with water that's as hot as I'm comfortable splooshing around in. I never use more than one sink's-worth since, as I already mentioned, I don't have much crockery anyway.
To work out how much energy it takes for me to wash up we need two things: the amount of water, and the temperature increase of the water.
For the amount I filled the sink using my kettle. It took a total of six kettle-cycles. Each cycle I weighed the kettle before and after and recorded the weight difference. Adding up all of these differences gave me the total weight of water that went into the sink: $10.234\ {\rm kg}$.
The temperature I find comfortable in the sink is $38^{\circ} {\rm C}$, which is a raise of $18^{\circ} {\rm C}$ (or 18 Kelvin) above room temperature.
A quick skim of the Web reveals that the specific heat capacity of water at this temperature is $4179.6\ {\rm J}\ {\rm kg}^{-1}\ {\rm K}^{-1}$.
So, to calculate the energy $E_S$ required (where $S$ stands for sink), we need to multiply everything together like so.
\begin{align}
E_S &= 4179.6\ {\rm J}\ {\rm kg}^{-1}\ {\rm K}^{-1} \times 10.234\ {\rm kg} \times 18\ {\rm K} \\
&= 769932\ {\rm J} \\
&= 770\ {\rm kJ}.
\end{align}
That's the first half of our comparison. Now we need the energy $E_D$ used by the dishwasher (I'll leave you to figure out what the $D$ stands for). The diswasher is an AEG F77420W0P (energy efficiency class A++) and luckily the dishwasher manual has a handy table that lists the energy requirements of the different modes. The table only has the values in kilowatt hours, but this is just a different unit for measurement energy. In fact $1\ {\rm kWh} = 3.6 \times 10^6\ {\rm J}$, so we can calculate the kJ by multiplying the kWh values by 3600.
| Mode | Energy (kWh) | Energy (kJ) | Water (l) |
|---|---|---|---|
| ECO | 0.7 | 2520 | 9.9 |
| Auto | 0.5 — 1.2 | 1800 — 4320 | 6.0 — 11.0 |
| PRO | 1.3 — 1.4 | 4680 — 5040 | 11.0 — 13.0 |
I don't know what these different modes — ECO, Auto and PRO — are for, but let's assume we'd be using the ECO setting. This means that for my dishwasher, in ECO mode, we have $E_D = 2520\ {\rm kJ}$.
And now we have what we need to do a comparison.
A washing up session takes $770\ {\rm kJ}$ whereas a dishwasher load takes $2520\ {\rm KJ}$; one dishwasher load is the equivalent of 3.27 sinks of washing up. My dishwasher is of the slim variety, but it still holds up to 14 plates, plus a bunch of other stuff. So if I wash at least 5 plates with each sink of water, then the sink will end up being more ecological in the long run. That's not unreasonable and suggests to me that in fact, the sink and dishwasher are fairly similar in terms of their energy use.
However, another factor is the water usage. The manual states that 9.9 litres of water are needed for an ECO load. That's the same amount as a single dish washing session in the sink, so the comparison here is in favour of the dishwasher.
To summarise, it does indeed seem that if you're doing a full load, you'd be better off (environmentally speaking) using the dishwasher. If you're doing less than a full load, the sink could well be better.
None of this includes the energy needed to build the dishwasher. According to this article in The Guardian, for an appiance that lasts 10 years this could add an extra 20% environmental cost, but I've not seen the calcuations and I couldn't find the actual figures for my dishwasher, so I'm not including that here.
These numbers are also all rather specific to my situation of course. A bigger dishwasher might be more efficient. For me, it's a little academic, since it would impossible for me to fill the dishwasher, so the future for me is clear: more washing up.
One of the encouraging things about this process is that it seems to have worked. If I look at my waste output between mid-August and mid-October 2020 and compare it to the same period last year, my output has reduced from an average of 366 g per day to 126 g per day, a two thirds decrease. Here’s the breakdown of how the two years compare across the categories.
I’ve been using a variety of different techniques to achieve this. For example my tolerance for eating food past it’s best-before date has increased considerably. There’s a sticker above my letter box asking not to receive any junk mail. I also buy food with lighter packaging: cardboard packets of beans instead of tins, cartons of wine instead of bottles. Wherever possible I buy plastic pots and bottles instead of glass.
Glass is really heavy, so cutting it out has been a really easy way to reduce the weight of my waste and as you can see from the graph, this is where I made my biggest decrease. But for many this choice will seem controversial, and many times when I’ve picked a plastic bottle from the shelf at the grocer instead of glass, I’ve wondered whether I was driven more by hitting my weight targets than any real environmental benefits.
So I thought I’d better look into the relative environmental impacts of glass as compared to plastic. Plastic has had a bad rap recently for having a terrible impact on the marine environment. But this is rather emotive, and is only one facet of the environmental impact of a product. Actually figuring out the full life cycle environmental impact of something is fiendishly difficult. You have to consider the production costs, transportation costs, recycling costs and much more besides. Happily Roberta Stefanini, Giulia Borghesi, Anna Ronzano and Giuseppe Vignali from the University of Parma have done all of this hard work already. Their paper “Plastic or glass: a new environmental assessment with a marine litter indicator for the comparison of pasteurized milk bottle”, recently published in the International Journal of Life Cycle Assessment, compares the environmental impact of glass and plastic polyethylene terephthalate (PET) across a range of environmental factors for the full life cycle of the packaging. This includes comparing non-recycled PET with recycled PET (R-PET) bottles, as well as non-returnable glass and returnable glass bottles.
The indicators used for comparison are “global warming (kg CO2 eq), stratospheric ozone depletion (kg CFC11 eq), terrestrial acidification (kg SO2 eq), fossil resource scarcity (kg oil eq), water consumption (m3) and human carcinogenic toxicity (kg 1.4-DCB)”. In addition they also introduce a new marine litter indicator (MLI).
What they find is surprisingly clear-cut. Across all of the indicators apart from MLI the same pattern emerges: R-PET is the least environmentally damaging, followed by PET. Returnable glass bottles follow, with non-returnable glass bottles the worst by a large margin. We can see this in the six graphs below. There’s a lot of detail in them, but I wanted to include them in full because it’s fascinating to see both how complex the results are and also how the different processes contribute to the final environmental cost. But in spite of the detail the overall conclusion from each graph is clear: non returnable glass is worse than the others (in all of the graphs higher is worse).
It’s a surprising definitive set of results. So why is it like this? The authors of the paper put this more clearly and succinctly than I could manage.
It’s worth noting that in the case of returnable glass bottles the authors assume that a bottle is reused eight times before having to be recycled. This is the number of reuses after which a bottle is likely to become broken or too scuffed to be used again. They determine that a bottle would have to be reused thirty times before its global warming potential reaches similar levels to those of a PET bottle, at which point the other criteria would still be worse environmentally.
The remaining criterion, not shown in these graphs, is that of the MLI. Here things change. MLI is proposed in the paper as an approach to comparing the relative impact on the marine ecosystem of the different packaging types. MLI is defined as follows:
$$
{\rm MLI} = \frac{F_1^{f_1} \times F_4^{f_4}}{F_2^{f_2} \times F_3^{f_3}}
$$
where $F_1$ is the number of disbursed containers, $F_2$ is the incentive for returning a bottle (e.g. the cash given for returning it), $F_3$ is the weight of the packaging material and $F_4$ is the material degradation over time (400 years in the case of glass, 100 years for PET). The values $f_1, \ldots, f_4$ are weights used to capture the relative importance of each of the four inputs.
The results for various weightings are given in this table (taken from the paper but amended slightly for clarity). As with the graphs, a higher number is environmentally worse.
| MLI weights $f_1, \ldots, f_4$ | PET | R-PET | Non-returnable glass | Returnable glass |
|---|---|---|---|---|
| 3, 2, 1, 2 | 0.56 | 0.56 | 19.47 | 0.78 |
| 2, 2, 1, 1 | 5.56 | 5.56 | 21.16 | 0.85 |
| 1, 1, ½, 1 | 0.75 | 0.75 | 4.60 | 0.92 |
| 2, 2, ½, 1 | 1.24 | 1.24 | 21.16 | 0.85 |
| 2, 3, 1, 2 | 0.93 | 0.93 | 105.80 | 0.85 |
This table shows that independent of the weights applied, non-returnable glass has the highest environmental impact. However, the comparison between R-PET and returnable glass is more nuanced. The authors conclude the following:
The paper is thorough and we’ve covered a lot of detail here, but the conclusion for me is much simpler: from an environmental perspective returnable PET plastic is clearly better than glass across multiple criteria. The only place where this doesn’t apply is for MLI, for which it’s much harder to make definitive judgements.
It seems therefore, that I should carry on choosing plastic packaging over glass whenever possible. That will benefit both my weight targets and the environment.
Total period: 2019-08-11 - 2020-08-11 (366 days)
Overall daily average: 231.22 g/day
Year 2019 daily average: 304.18 g/day
Year 2020 daily average: 187.57 g/day
So it seems my average daily output of waste is around 230g/day. It'll be interesting to discover whether that goes down as a result of me recording and keeping track of the data, but if you look at the graphs you can see a big chunk happens around Christmas, so my relatively low average for 2020 will inevitably go up.
Here are a couple of graphs that show the same data plotted as a histogram and then as a histocurve. You may recall that our starting point was a realisation that simply plotting the data and joining the points gave a misleading representation of the data. The important point about these two graphs — both the histogram and the histocurve — is that the area under the graph is always a good representation of the actual quantities the data represents. In this case, it's how much recycling and rubbish I generate each day.
Having got to this point, we can see that there are also some pitfalls with using these histocurves that don't apply to histograms. I reckon it's important to be aware of them, so worth spending a bit of time considering them.
The most obvious to me is the fact that the histocurve doesn't respect the maximum or minimum bounds of the graph. In the case of my waste data, there's a very clear minimum floor because it's impossible for me to generate negative waste.
In spite of this, because the height is higher at some points than it would otherwise be as a means of maintaining continuity, it has to be lower at other points to compensate. As a result in several areas the height dips below the zero point. We can see this in the stacked curve as areas where the curve gets 'cut off' by the curve below it.
As yet, I've not been able to think of a sensible way to address this. Fixing it would require compensating for overflow in some areas by distributing the excess across other columns. This reduces accuracy and increases complexity. It's also not clear that an approach like this could always work. If you have any ideas, feel free to share them in the comments.
For some types of data this is more important than others. For example, in the case of this waste data, the notion of negative waste is pretty perplexing, however for many types of data there is no strict maximum or minimum to speak of. Suppose for example it were measurements of water flowing in and out of a reservoir. In this case the issue would be less relevant.
Another danger is that the graph gives a false impression of accuracy. The sharp boundaries between columns in a histogram make clear where a data value starts and ends. By looking at the graph you know over which period a reading applies. With a histocurve it looks like you should be able to read a value off the graph for any given day. The reading would be a 'prediction' based on the trends, but of course we've chosen the curve of the graph in order to balance the area under the curve, rather than using any consideration of how the curve relates to the phenomenon being measured.
This leads us on to another issue: that it's hard to derive the actual readings. In the case of a histogram we can read off the height and width of a column and reverse engineer the original reading by multiplying the two together. We aren't able to do this with the histocurve, so the underlying data is more opaque.
The final problem, which I'd love to have a solution for, is that changing the frequency of readings changes the resulting curve. The current data shows readings taken roughly once per week at the weekends. Suppose I were to start taking readings mid-week as well. If the values taken midweek were exactly half the values I was measuring before (because they were taken twice as frequently) then the histogram would look identical. The histocurve on the other hand would change.
These limitations aren't terminal, they just require consideration when choosing what type of graph to use, and making clear how the viewer should interpret it. The most important characteristic of the histocurve is that it captures the results by considering the area under the curve, and none of the values along the curve itself are truly representative of the actual readings taken beyond this. As long as this is clear then there's probably a use for this type of graph out there somewhere.
That wraps up this discussion about graphs, histgrams and histocurves. If you made it this far, as Chris Mason would say, congratulations: you ooze stamina!
In part two we found out we could draw a continuous line graph that captured several useful properties that are usually associated with histograms, notably that the area under the line graph is the same as it would be for a histogram between the measurement points along the $x$-axis.
But what if we want to go a step further and draw a smooth line, rather than one made up of straight edges? Rather than just a continuous line, can we present the same data with a continuously differentiable line? Can we do this and still respect this 'area under the graph' property?
It turns out, the answer is "yes"! And we can do it in a similar way. First we send the curve through each of the same points at the boundary of each column, then we adjust the height of the midpoint to account for any changes caused by the curvature of the graph.
There are many, many, ways to draw nice curves, but one that frequently comes up in computing is the Bézier curve. It has several nice properties, in that it's nicely controllable, and depending on the order of the curve, we can control to any depth of derivative we choose. We'll use second-degree Bézier curves, meaning that we'll be able to have a continuous line and a continuous first derivative. This should keep things nice and smooth.
Bézier curves are defined parametrically, meaning that rather than having a function that takes an $x$ input and produces a $y$ output, as is the common Cartesian case, instead it takes a parameter input $t$ that falls between 0 and 1, and outputs both the $x$ and $y$ values. In order to avoid getting confused with the variables we used in part two, we're going to use $u$ and $v$ instead of $x$ and $y$ respectively.
Here's the formula for a second-order Bézier curve.
$$
\begin{pmatrix} u \\ v \end{pmatrix} = (1 - t)^3 \begin{pmatrix} u_0 \\ v_0 \end{pmatrix} + 3(1 - t)^2 t \begin{pmatrix} u_1 \\ v_1 \end{pmatrix} + 3 (1 - t) t^2 \begin{pmatrix} u_2 \\ v_2 \end{pmatrix} + t^3 \begin{pmatrix} u_3 \\ v_3 \end{pmatrix} .
$$
Where $\begin{pmatrix} u_0 \\ v_0 \end{pmatrix}$, $\begin{pmatrix} u_3 \\ v_3 \end{pmatrix}$ are the start and end points of the curve respectively, and $\begin{pmatrix} u _1\\ v_1 \end{pmatrix}$, $\begin{pmatrix} u_2 \\ v_2 \end{pmatrix}$ are control points that we position in order to get our desired curve.
The fact a Bézier curve is parametric is a problem for us, because it makes it considerably more difficult to integrate under the graph. If we want to know the area under the curve, we're going to have to integrate it, so we need a way to turn the parameterised curve into a Cartesian form.
Luckily we can cheat.
If we set $\begin{pmatrix} u_1 \\ v_1 \end{pmatrix}$ and $\begin{pmatrix} u_2 \\ v_2 \end{pmatrix}$ to be $\frac{1}{3}$ and $\frac{2}{3}$ of the way along the curve respectively, then things get considerably easier. In other words, set
\begin{align*}
u_1 & = u_0 + \frac{1}{3} (u_3 - u_0) \\
& = \frac{2}{3} u_0 + \frac{1}{3} u_3 \\
\end{align*}
and
\begin{align*}
u_2 & = u_0 + \frac{2}{3} (u_3 - u_0) \\
& = \frac{1}{3} u_0 + \frac{2}{3} u_3 .
\end{align*}
Substituting this into our Bézier curve equation from earlier we get
\begin{align*}
u & = (1 - t)^3 u_0 + 3 (1 - t)^2 t \times \left( \frac{2}{3} u_0 + \frac{1}{3} u_3 \right) + 3 (1 - t) t^2 \times \left( \frac{1}{3} u_0 + \frac{2}{3} u_3 \right) + t^3 u_3 \\
& = u_0 + t (u_3 - u_0) .
\end{align*}
When we choose our $u_1$ and $u_2$ like this, we can perform the substitution
$$
\psi(t) = u_0 + t(u_3 - u_0)
$$
in order to switch between $t$ and $u$. This will make the integral much easier to solve. We note that $\psi$ is a bijection and so invertible as long as $u_3 \not= u_0$. We can therefore define the inverse:
$$
t = \psi^{-1} (u) = \frac{u - u_0}{u_3 - u_0} \\
$$
It will also be helpful to do a bit of groundwork. We find the values at the boundary as
\begin{align*}
\psi^{-1} (u_0) & = 0, \\
\psi^{-1} (u_3) & = 1, \\
\end{align*}
and we also define the following for convenience.
$$
V(u) = v(\psi^{-1} (u)) .
$$
We'll use these in the calculation of the integral under the Bézier curve, which goes as follows.
$$
\int_{u_0}^{u_3} V(u) \mathrm{d}u
$$
Using the substitution rule we get
\begin{align*}
\int_{\psi^{-1}(u_0)}^{\psi^{-1}(u_3)} & V(\psi(t)) \psi'(t)\mathrm{d}t = \int_{t = 0}^{t = 1} v(\psi^{-1}(\psi(t))) (u_3 - u_0) \mathrm{d}t \\
& = (u_3 - u_0) \int_{0}^{1} v(t) \mathrm{d}t . \\
& = (u_3 - u_0) \int_{0}^{1} (1 - t)^3 v_0 + 3 (1 - t)^2 t v_1 + 3 (1 - t) t^2 v_2 + t^3 v_3 \mathrm{d}t \\
& = (u_3 - u_0) \int_{0}^{1} (1 - 3t + 3t^2 - t^3) v_0 + 3 (t - 2t^2 + t^3) v_1 + 3 (t^2 - t^3) v_2 + t^3 v_3 \mathrm{d}t \\
& = \frac{1}{4} (u_3 - u_0) (v_0 + v_1 + v_2 + v_3) .
\end{align*}
We'll bank this calculation and come back to it. Let's now consider how we can wrap the Bézier curve over the points in our graph to make a nice curve. For each column we're going to end up with something like this.
Now as before, we don't have control over $u_0$, $v_0$ because it affects the adjoining curve. We also don't have control over $u_1$ and $u_2$ because as just described, we have these set to allow us to perform the integration. We also must have $u_3$ set as $u_3 = u_0 + w / 2$ so that it's half way along the column.
Our initial assumption wil be that $v_3 = h$, but this is the value we're going to manipulate (i.e. raising or lowering the central point) in order to get the area we need. We shouldn't need to adjust it by much.
That just leaves $v_1$ and $v_2$. We need to choose these to give us a sensible and smooth curve, which introduces some additonal constraints. We'll set the gradient at the point $u_0$ to be the gradient $g_1$ of the line that connects the heights of the centrepoints of the two adjacent columns:
$$
g_1 = \frac{y - y_L}{x - x_L}
$$
where $x, y$ are the same points we discussed in part two, and $x_L, y_L$ are the same points for the column to the left. We'll also use $x_R, y_R$ to refer to the points for the column on the right, giving us:
$$
g_2 = \frac{y_R - y}{x_R - x} .
$$
Using our value for $g_1$ we then have
$$
v_1 = v_0 + g_1 (u_1 - u_0) .
$$
For the gradient $g$ at the centre of the column, we set this to be the gradient of the line between $y_1$ and $y_2$:
$$
g = \frac{y_2 - y_1}{x_2 - x_1} .
$$
We then have that
$$
v_2 = v_3 + g (u_2 - u_3) .
$$
From these we can calculate the area under the curve using the result from our integration calculation earlier, by simply substiuting the values in. After simplifying the result, we get the following.
$$
A_1' = \frac{1}{8}(x_2 - x_1) \left( 2y' + \frac{13}{6} y_1 - \frac{1}{6} y_2 + \frac{1}{6} g_1 (x_2 - x_1) \right)
$$
where $y'$ is the height of the central point which we'll adjust in order to get the area we need. This looks nasty, but it'll get simpler. We can perform the same calculation for the right hand side to get
$$
A_2' = \frac{1}{8}(x_2 - x_1) \left( 2y' + \frac{13}{6} y_2 - \frac{1}{6} y_1 - \frac{1}{6} g_2 (x_2 - x_1) \right) .
$$
Adding the two to give the total area $A' = A_1' + A_2'$ allows us to do a bunch of simplification, giving us
$$
A' = \frac{w}{2} \left( \frac{1}{2} y_1 + \frac{1}{2} y_2 + y' \right) + \frac{w^2}{48} (g_1 - g_2) .
$$
If we now compare this to the $A$ we calculated for the straight line graph in part two, subtracting one from the other gives us that
$$
y' = y + \frac{w}{24} (g_2 - g_1) .
$$
This tells us how much we have to adjust $y$ by to compensate for the area change caused by the curvature of the Bézier curves.
What does this give us in practice? Here's the new smoothed graph based on the same data as before.
Let's overlay the three approaches — histogram, straight line and curved graphs — to see how they all compare. The important thing to note is that the area under each of the columns — bounded above by the flat line, the straight line and the curve respectively — are all the same.
Because of the neat way Bézier curves retain their area properties, we can even stack them nicely, similarly to how we stacked our histogram in part one, to get the following representation of the full set of data.
Putting all of this together, we now have a pretty straightforward way to present area-under-the-graph histograms of continuous data in a way that captures that continuity. I call this graph a "histocurve". A histocurve can give a clearer picture of the overall general trends of the data. For example, each of the strata in the histocurve remains unbroken, compared to the strata in a classic histogram which is liable to get broken at the boundary between every pair of columns.
That's all great, but it's certainly not perfect. In the fourth and final part of this series which I hope to get out on the 3rd December, I'll briefly discuss the pitfalls of histocurves, some of their negative properties, and things I'd love to fix but don't know how.
We finished by looking at how a histogram would be a good choice for representing the particular type of data I've been collecting, to express the quantity of various types of waste (measured by weight) as the area under the graph. Here's the example data plotted as a histogram.
While this is good at presenting the general picture, I really want to also express how my waste generation is part of a continuous process. In the very first graph I generated to try to understand my waste output, I drew the datapoints and joined them with lines. This wasn't totally crazy as it highlighted the trends over time. However, it gave completely the wrong impression because the area under the graph bore no relation to the amount of waste I produced.
How can we achieve both? Show a continuous change of the data by joining datapoints with lines, while also ensuring the area under the graph represents the actual amount of waste produced?
The histogram above achieves the goal of having the area under the graph represent the all-important quantities captured by the data clearly visible in the graph. But it doesn't express the continuous nature of the data.
Contrariwise, if we were to take the point at the top of each histogram column and join them up, we'd have a continuous line across the graph, but the area underneath would no longer represent useful data.
If we want to capture a `middle ground' between the two, it's helpful to apply some additional constraints.
- The line representing the weights should be continuous.
- The area under the line should be the same as the area under the histogram column for each column individually.
- For each reading, the line can be affected by the readings either side (this is inevitable if the constraint 1 is going to be enforced), but should be independent of anything further away.
To do this, we'll adjust the position of the datapoints for each of the readings and introduce a new point in between every pair of existing datapoints as follows.
- Start with the datapoints positioned to be horizontally centred in each column and taken as the height of the histogram column that encloses it.
- For every pair of datapoints A and B, place an additional point at the boundary of the columns for A and B, and with y value set as the average between the two columns A and B.
Following these rules we end up with something like this.
This gives us our continuous line, but as you can see from the diagram, for each column the area under the line doesn't necessarily represent the quantity captured by the data. We can see this more easily by focussing in on one of the columns. The hatched area in the picture below shows area that used to be included, but which would be removed if we drew our line like this, making the area under the line for this particular region less than it should be.
Across the entire width of these graphs the additions might cancel out the subtractions, but that's not guaranteed, and it also fails our second requirement that the area under the line should be the same as the area under the histogram column for each column individually.
To address this we can adjust the position of the point in the centre of each column by altering its height to capture the correct amount of area. In the case shown above, we'd need to move the point higher because we've cut off some of the area and need to get it back. In other cases we may need to reduce the height of the point to remove area that we over-captured.
To calculate the exact height of the central point, we can use the following formula.
$$ y = 2h - \frac{1}{2} (y_1 + y_2) .
$$
The area $A = A_1 + A_2 + A_3 + A_4$ under the curve can then be calculated as follows.
\begin{align*} A & = \left( \frac{w}{2} \times y_1 \right) + \left( \frac{w}{2} \times y_2 \right) + \left( \frac{1}{2} \times \frac{w}{2} \times (y - y_1) \right) + \left( \frac{1}{2} \times \frac{w}{2} \times (y - y_3) \right) \\ & = \frac{w}{2} \left( \frac{1}{2} y_1 + \frac{1}{2} y_2 + y \right) . \\ \end{align*}
Substituting $y$ into this we get the following.
\begin{align*} A & = \frac{w}{2} \left( \frac{1}{2} y_1 + \frac{1}{2} y_2 + 2h - \frac{1}{2} y_1 - \frac{1}{2} y_2 \right) \\ & = wh. \end{align*}
Which is the area of the column as required.
Following this approach we end up with a graph like this.
Which taken on its own gives a clear idea of the trend over time, while still capturing the overall quantity of waste produced in each period as the area under the graph.
In the next part we'll look at how we can refine this further by rendering a smooth curve, rather than straight lines, but in a way that retains the same properties we've been requiring here.
All of the graphs here were produced using the superb MatPlotLib and the equations rendered using MathJax (the first time I'm using it, and it looks like it's done a decent job).
You may think this is all self-evident, and that anyone taking the trouble to plot data in a graph will obviously have taken these things into account, but sadly it's rarely the case. I see data visualisation abominations on a daily basis. What's more it's often the people you'd expect to be best at it who turn out to fall into the worst traps. Over fifteen years of reviewing academic papers in computer science, I've seen numerous examples of terrible data visualisation. These papers are written by people who have both access to and competence in the best visualisation tooling, and who presumably have a background in analytical thinking, and yet graphs presented in papers often fail the most basic requirements. It's not unusual to see graphs that are too small to read, with unlabelled axes, missing units, use of colour in greyscale publications, or with continuous lines drawn between unrelated discrete data points.
And that's without even mentioning pseudo-3D projections or spider graphs.
One day I'll take the time to write up some of these data visualisation horror stories, but right now I want to focus on one of my own infractions. I'll warn you up front that it's not a pretty story, but I'm hoping it will have a happy ending. I'm going to talk about how I created a most terrible graph, and how I've attempted to redeem myself by developing what I believe is a much clearer representation of the data.
Over the last couple of months I've been collecting data on how much waste and recycling I generate. Broadly speaking this is for environmental and motivational reasons: I believe that if I make myself more aware of how much rubbish I'm producing, it'll motivate me to find ways to reduce it, and also help me understand where my main areas for improvement are. If I'm honest I don't expect it'll work (many years ago I was given a device for measuring real-time electricity usage with a similar aim and I can't say that succeeded), but for now it's important to understand my motivations. It goes to the heart of what makes a good graphing choice.
So, each week I weigh my rubbish using kitchen scales, categorised into different types matching the seven different recycling bins provided for use in my apartment complex.
Here's the data I've collected until now presented in a table.
| Date | Paper | Card | Glass | Metal | Returnables | Compost | Plastic | General |
|---|---|---|---|---|---|---|---|---|
| 18/08/19 | 221 | 208 | 534 | 28 | 114 | 584 | 0 | 426 |
| 25/08/19 | 523 | 304 | 702 | 24 | 85 | 365 | 123 | 282 |
| 01/09/19 | 517 | 180 | 0 | 0 | 115 | 400 | 0 | 320 |
| 06/09/19 | 676 | 127 | 360 | 14 | 36 | 87 | 0 | 117 |
| 19/09/19 | 1076 | 429 | 904 | 16 | 0 | 1661 | 0 | 417 |
| 28/09/19 | 1047 | 162 | 1133 | 105 | 74 | 341 | 34 | 237 |
| 05/10/19 | 781 | 708 | 218 | 73 | 76 | 1391 | 54 | 206 |
| 13/10/19 | 567 | 186 | 299 | 158 | 40 | 289 | 63 | 273 |
We can't tell a great deal from this table. We can certainly read off the measurements very easily and accurately, but beyond that the table fails to give any sort of overall picture or idea of trends.
The obvious thing to do is therefore to draw a graph and hope to tease out something that way. So, here's the graph I came up with, and which I've had posted and updated on my website for a couple of months.
What does this graph show? Well, to be precise, it's a stacked plot of the weight measurements against the dates the measurements were taken. It gives a pretty clear picture of how much waste I produced over a period of time. We can see that my waste output increased and peaked before falling again, and that this was mostly driven by changes in the weight of compost I produced.
Or does it? In fact, as the data accumulated on the graph, it became increasingly clear that this is a misleading visualisation. Even though it's an accurate plot of the measurements taken, it gives completely the wrong idea about how much waste I've been generating.
To understand this better, let's consider just one of the stacked plots. The red area down at the base is showing the measurements I took for general waste. Here's another graph that shows the same data isolated from the other types of waste and plotted on a more appropriate scale.
If you're really paying attention you'll notice that the start date on this second graph is different to that of the first. That's because the very first datapoint represents my waste output for the seven days prior to the reading, and we'll need those extra seven days for comparison with some of the other plots we'll be looking at shortly.
There are several things wrong with this plot, but the most serious issue, the one I want to focus on, is that it gives a completely misleading impression of how much waste I've been generating. That's because the most natural way to interpret this graph would be to read off the value for any given day and assume that's how much waste was generated that day. This would leave the area under the graph being the total amount of waste output. In fact the lines simply connect different data points. The actual datapoints themselves don't represent the amount of waste generated in a day, but in fact the amount generated in a week. And because I don't always take my measurements at the same time each week, they don't even represent a week's worth of rubbish. To find out the daily waste generated, I'd need to divide a specific reading by the number of days since the last reading.
Take for example the measurements taken on the 6th September. I usually weight my rubbish on a Saturday, but because I went on holiday on the 7th I had to do the weighing a day early. Then I was away from home for seven days, came back and didn't then weight my rubbish again until the 19th, nearly two weeks later.
Although I spent a chunk of this time away, it still meant that the reading was high, making it look as if I'd generated a lot of waste over the two-week period. In fact, considering this was double the time of the usual readings, it was actually a relatively low reading. This should be reflected in the graph, but it's not. It looks like I generated more rubbish than expected; in fact I generated less.
We can see this more clearly if we plot the data as a column (bar) graph and as a histogram. Here's the column graph first.
These are the same datapoints as in the previous graph, but drawn as columns with widths proportional to the duration that the readings represent. The column that spreads across from the 6th to the 19th September is the reading we've just been discussing. This is a tall, wide, column because it represents a long period (nearly two weeks) and a heaver than usual weight reading (because it's more than a weeks' worth of rubbish). If we now convert this into a histogram, it'll give us a clearer picture of how much waste was being generated per day.
This histogram takes each of the columns and divides it by the number of days the column represents. A histogram has the nice property that the area — rather than the height — of a column represents the value being plotted. In this histogram, the area under all of the columns represents the quantity of waste that I've generated across the entire period: the more blue, the more waste.
Not only is this a much clearer representation, it also completely changes the picture. The original graph made it look like my waste output peaked in the middle. There is a slight rise in the middle, but it's actually just a local maximum. In fact the overall trend was that my daily general waste output was decreasing until the middle of the period, and then rose slightly over time. That's a much more accurate reflection of what actually happened.
It would be possible to render the data as a stacked histogram, and to be honest I'd be happy with that. The overall picture, which ties in with my motivation for wanting the graph in the first place, indicates how much waste I'm generating based on the area under the graph.
But in fact I tend to be generating small bits of rubbish throughout the week, and I'd like to see the trend between readings, so it would be reasonable to draw a line between weeks rather than have them as histogram blocks or columns.
So this leads us down the path of how we might draw a graph that captures these trends, but still also retains the nice property that the area under the graph represents the amount of waste produced.
That's what I'll be exploring in part two.
All of the graphs here were generated using the superb MatPlotLib.





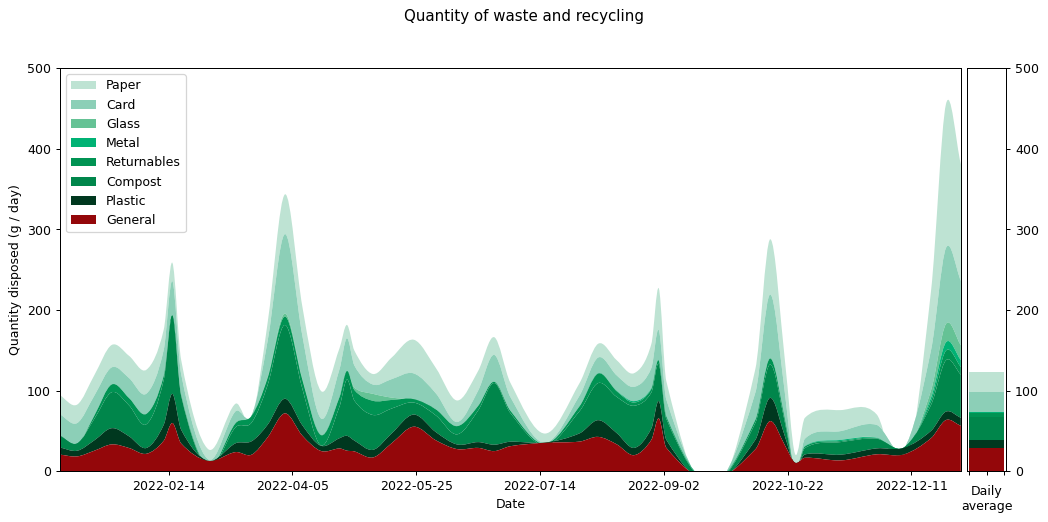
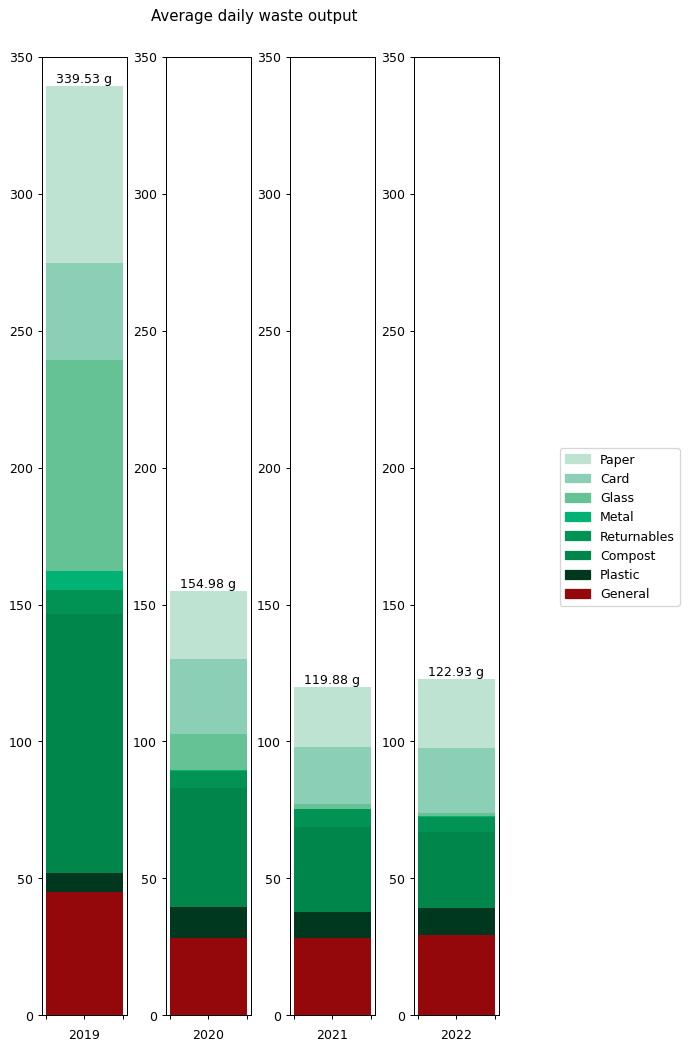
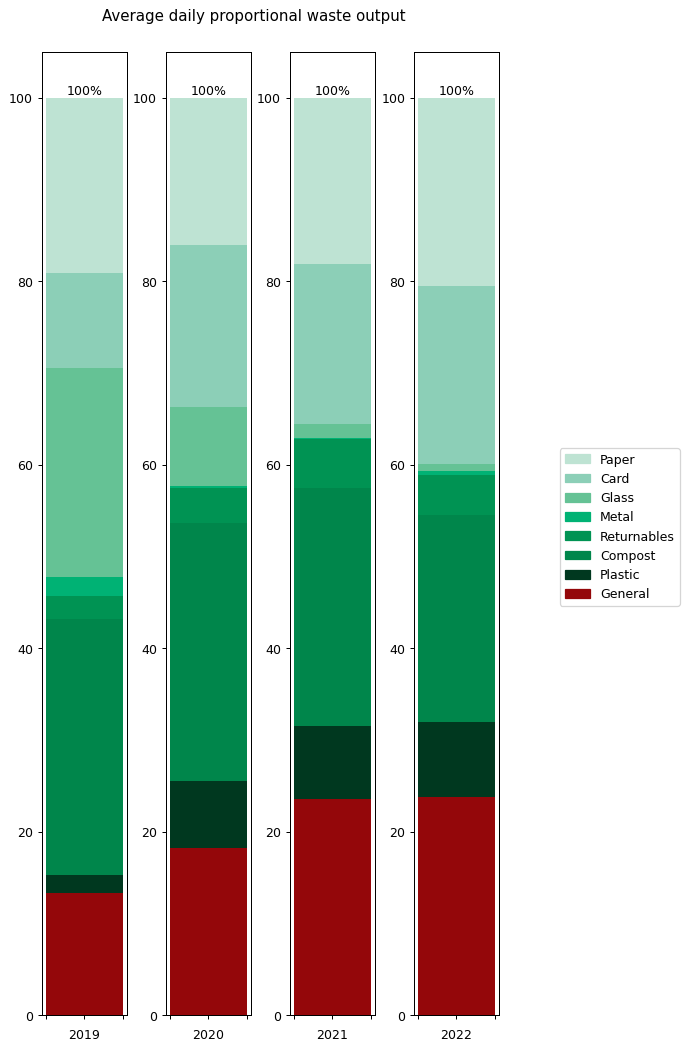
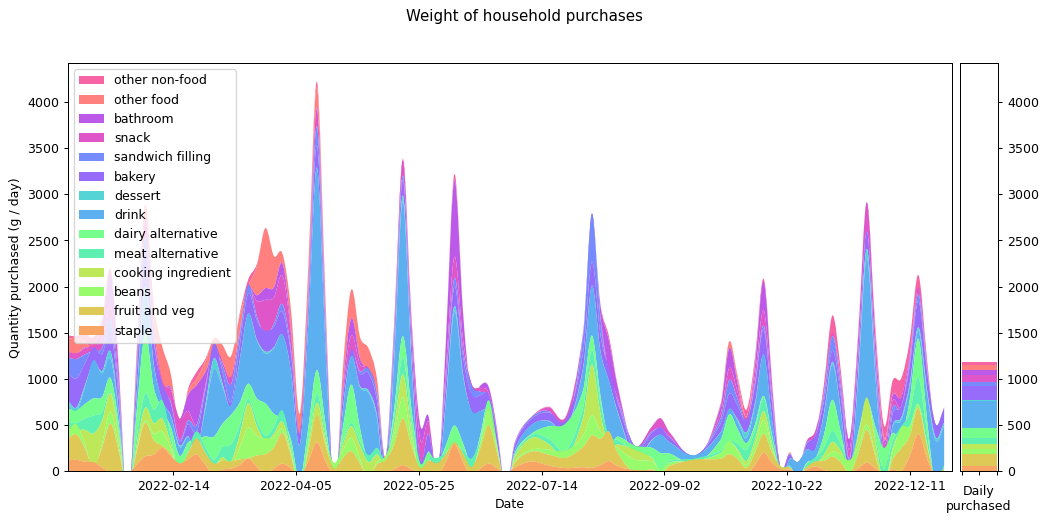
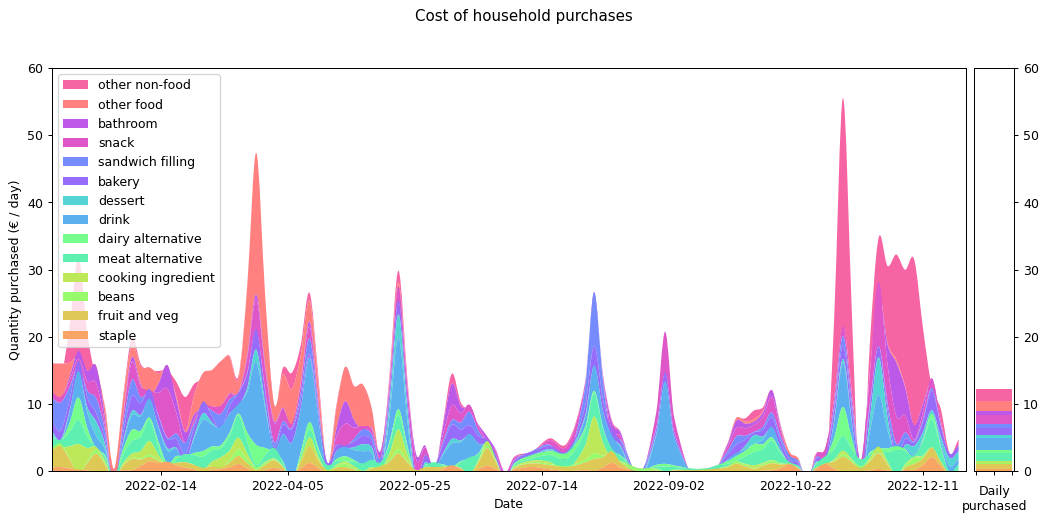
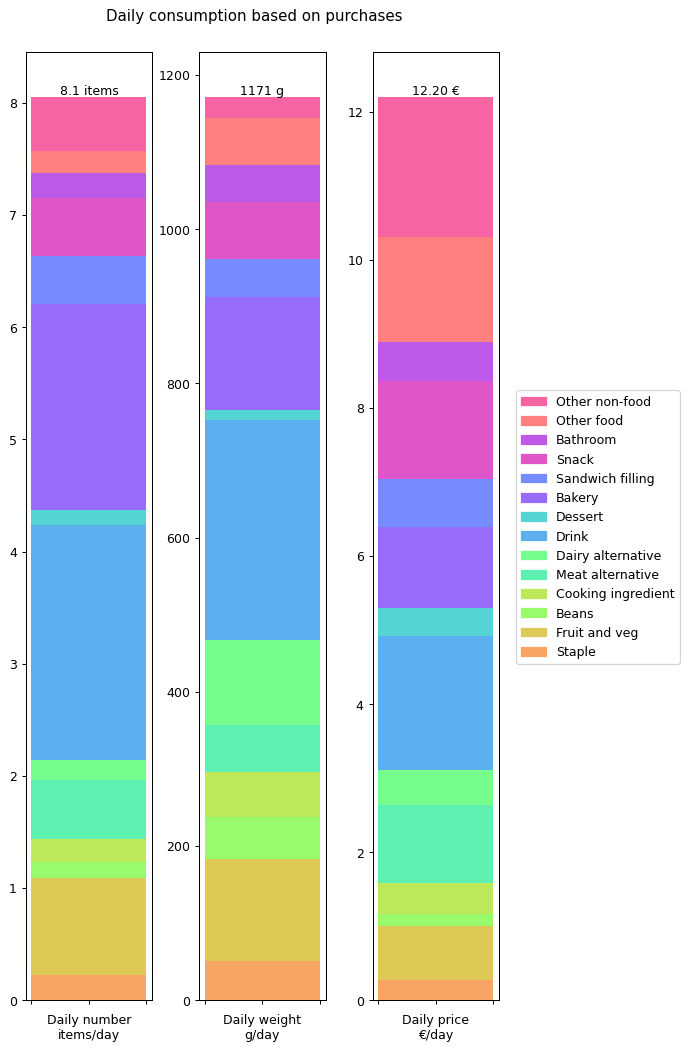
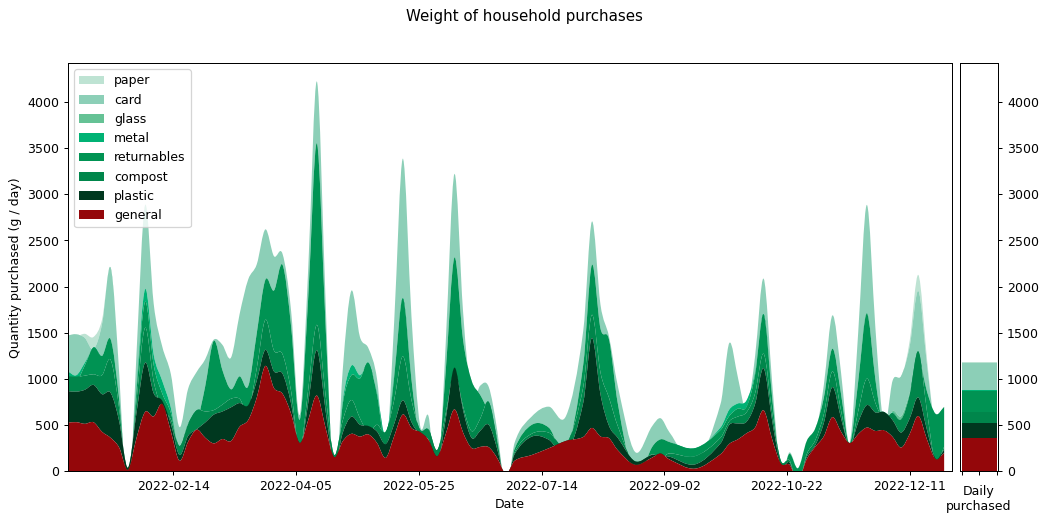
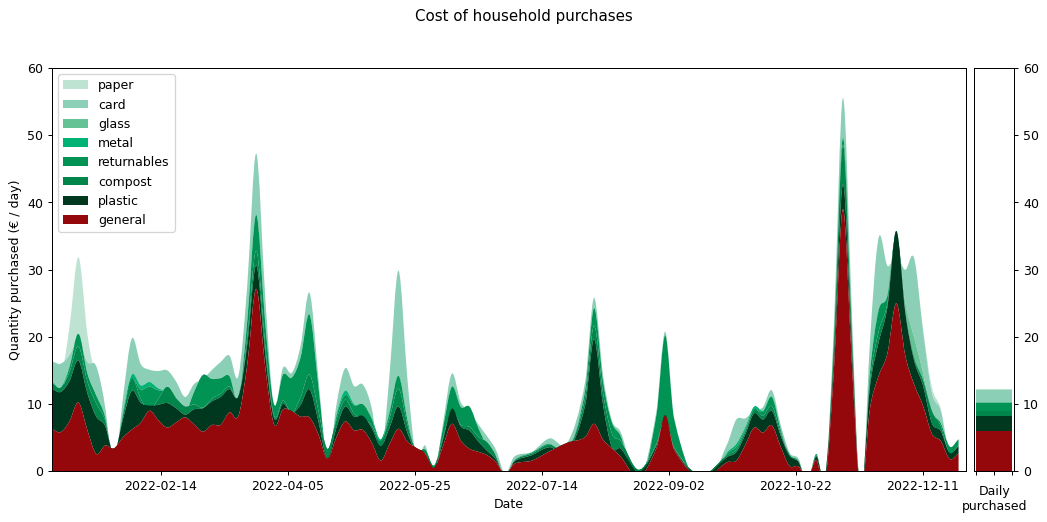
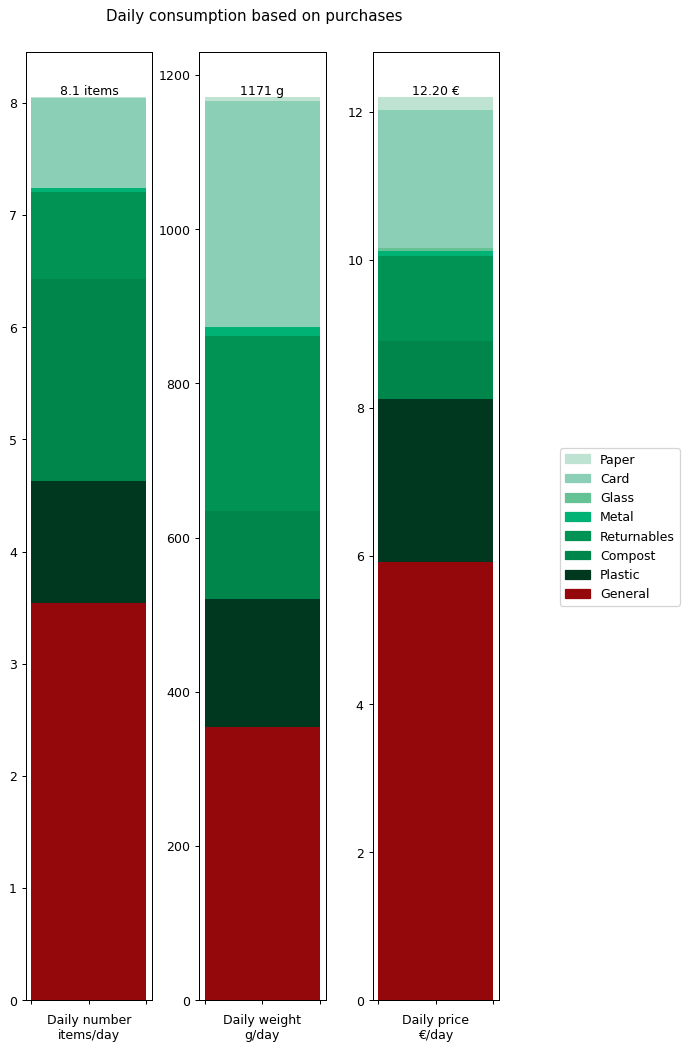
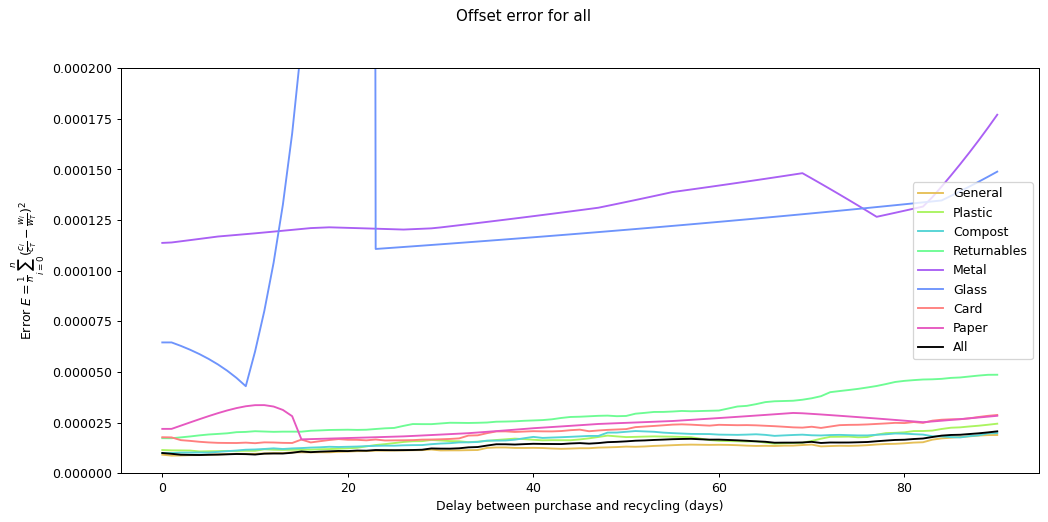
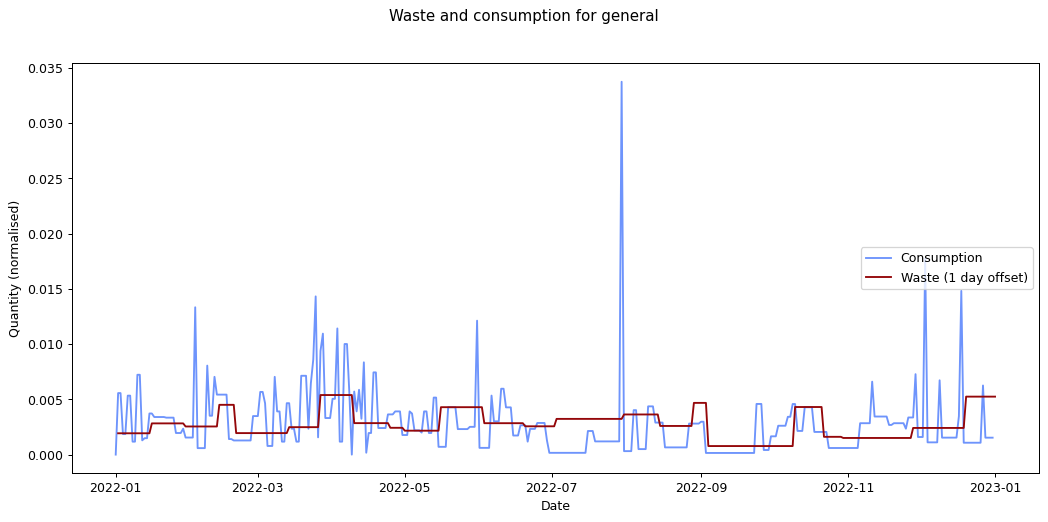
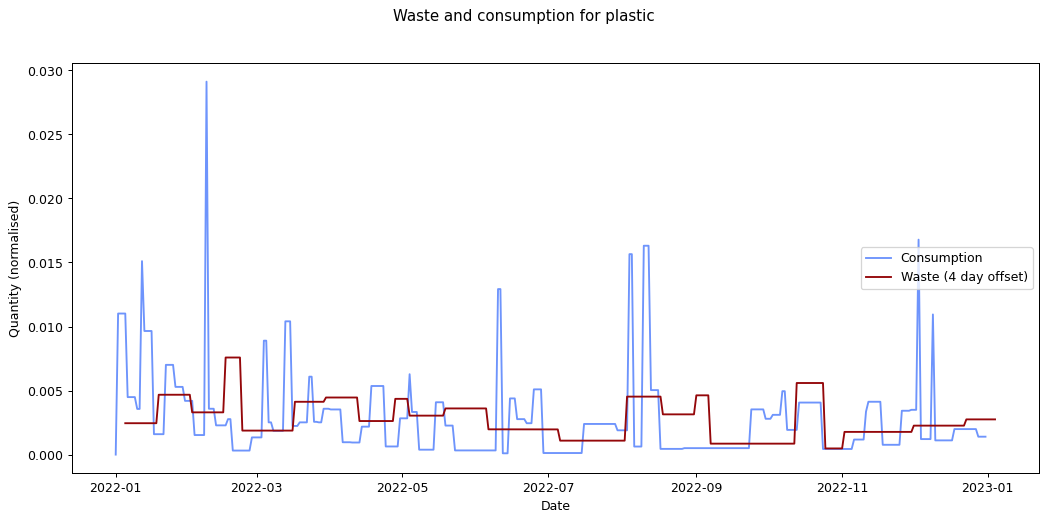
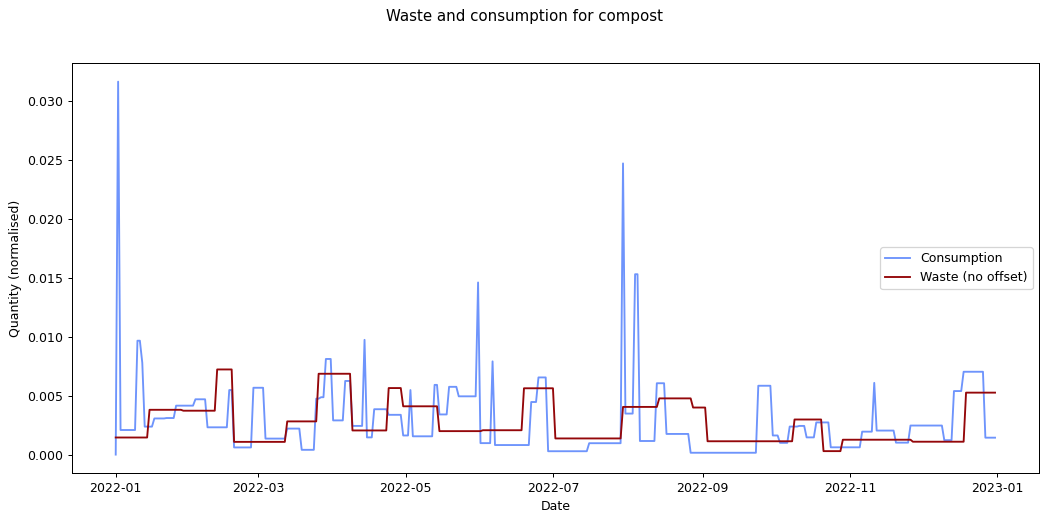
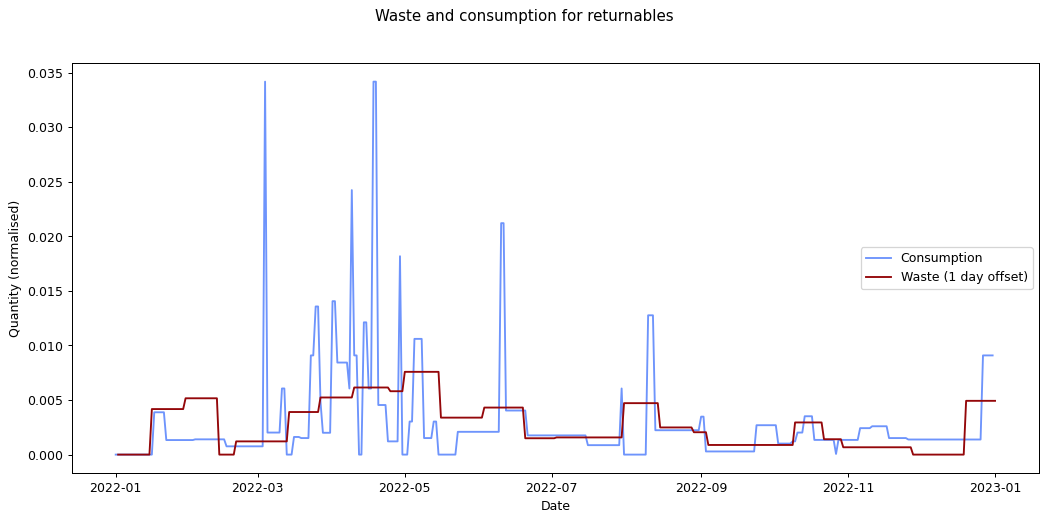
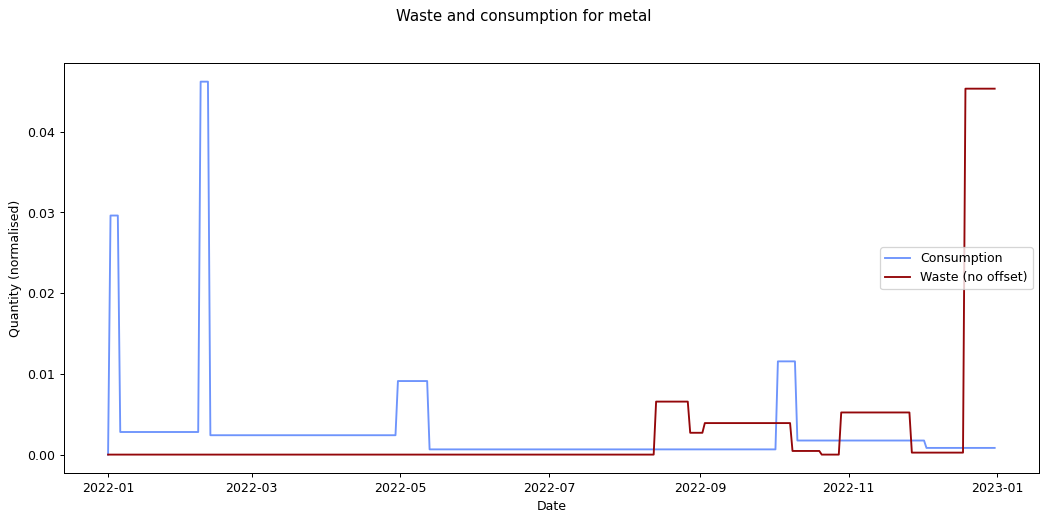
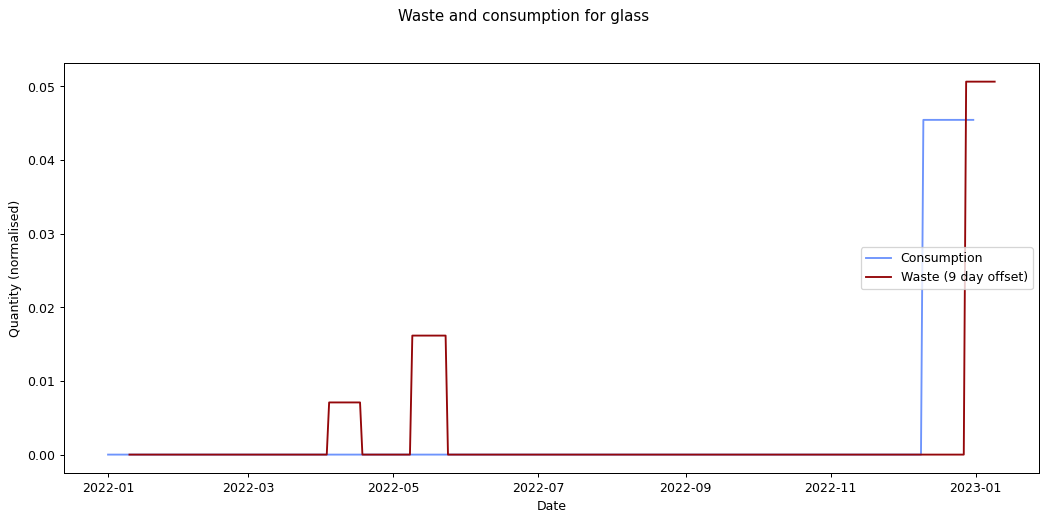
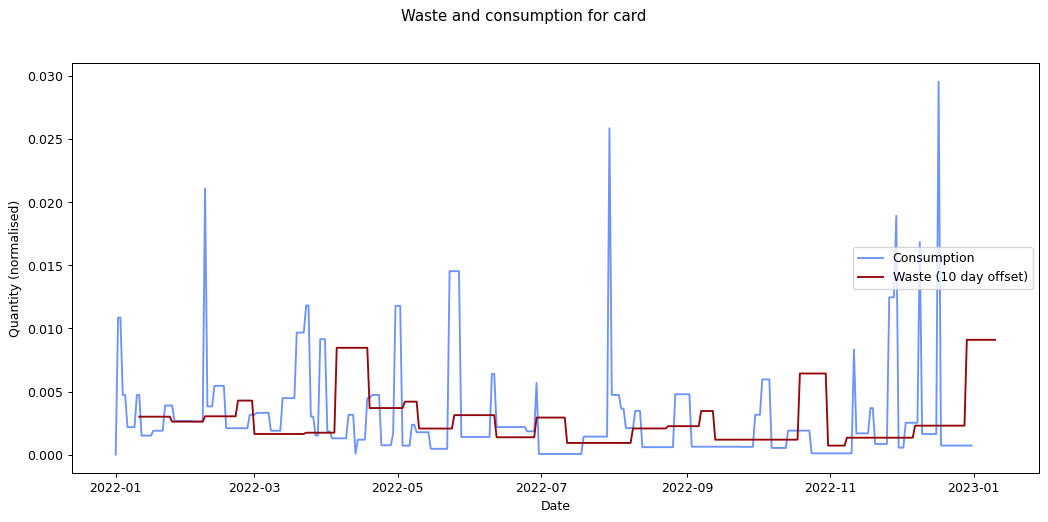
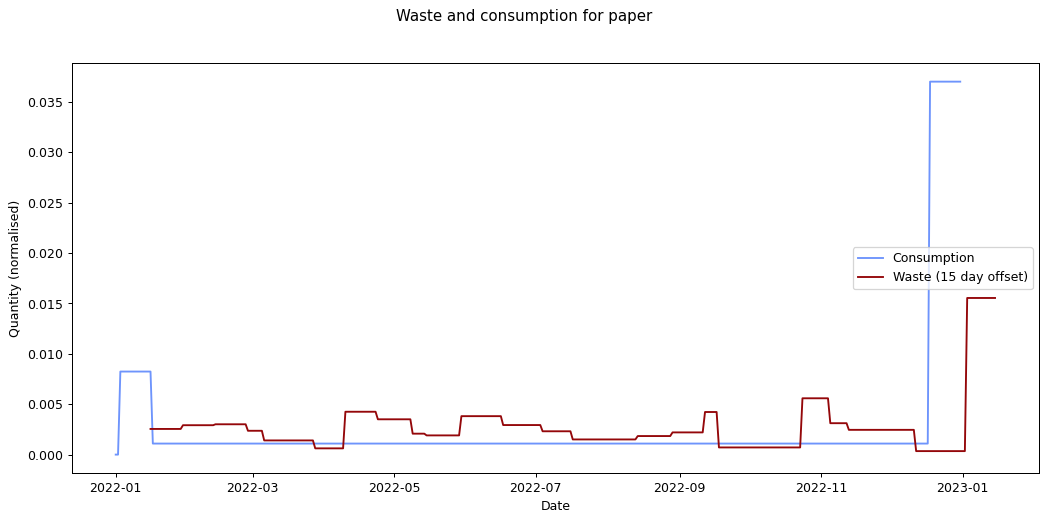
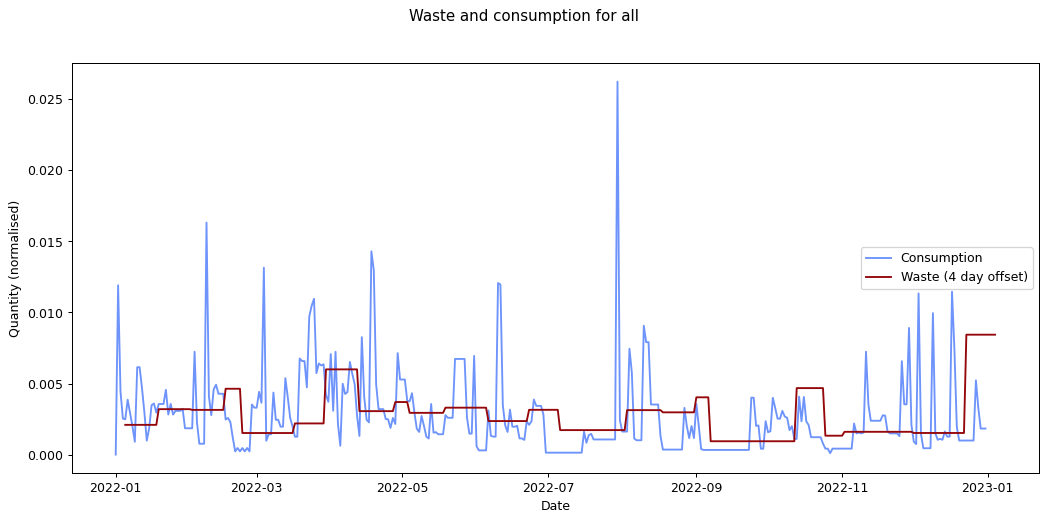


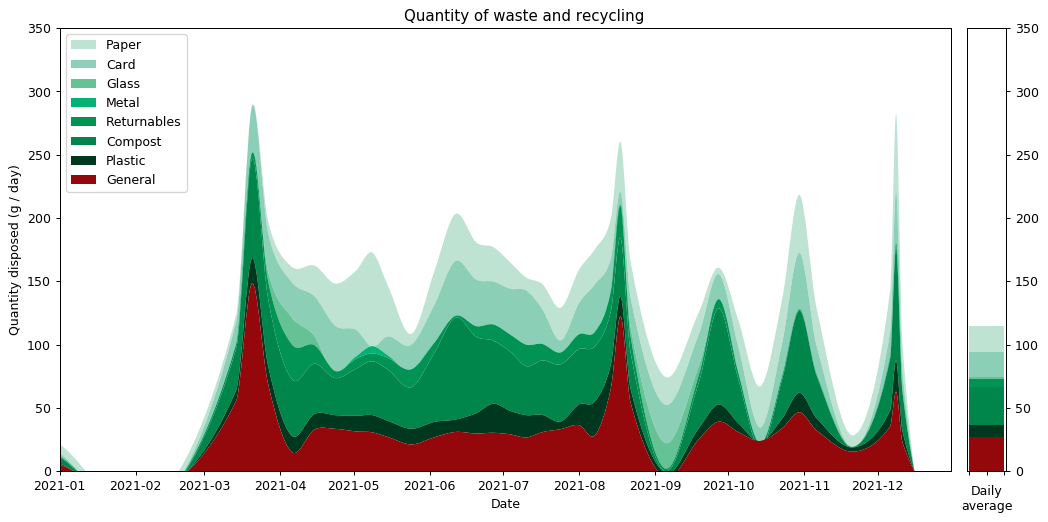
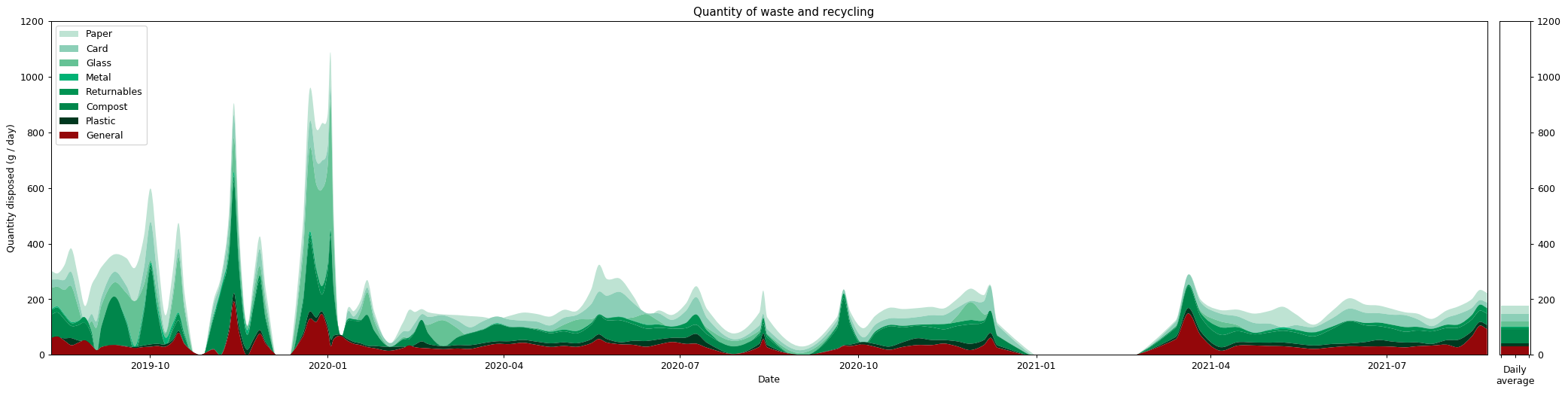




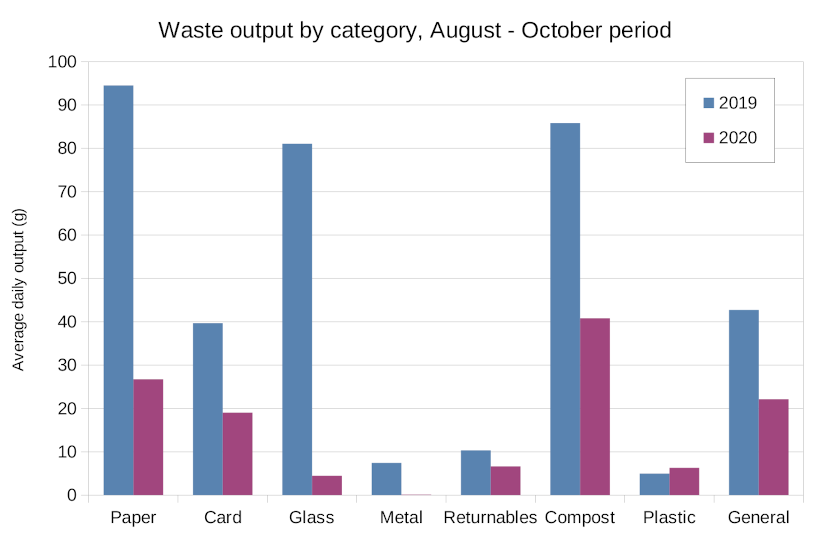
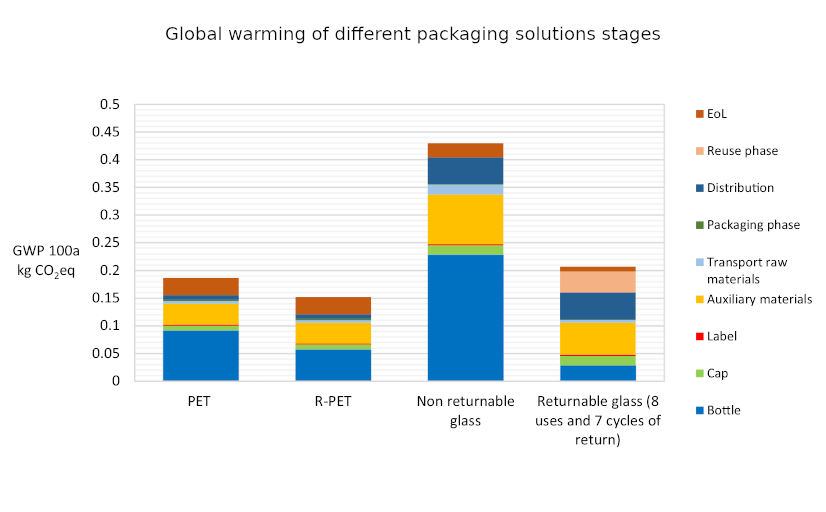
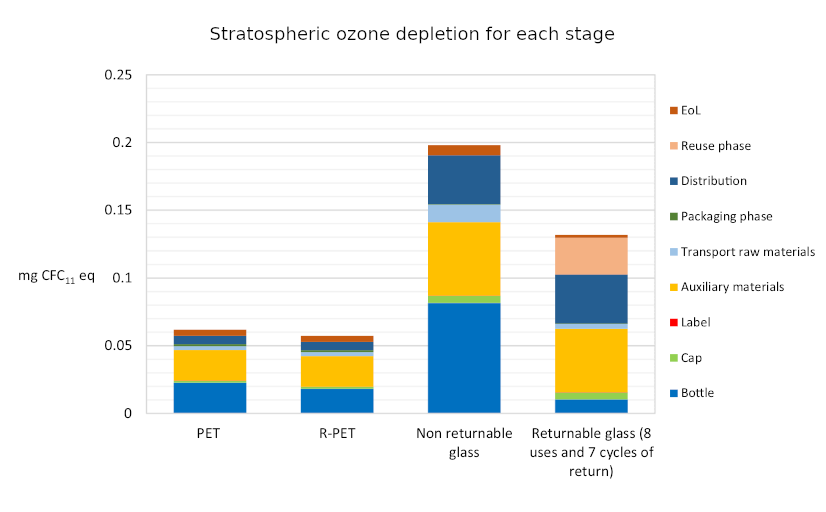
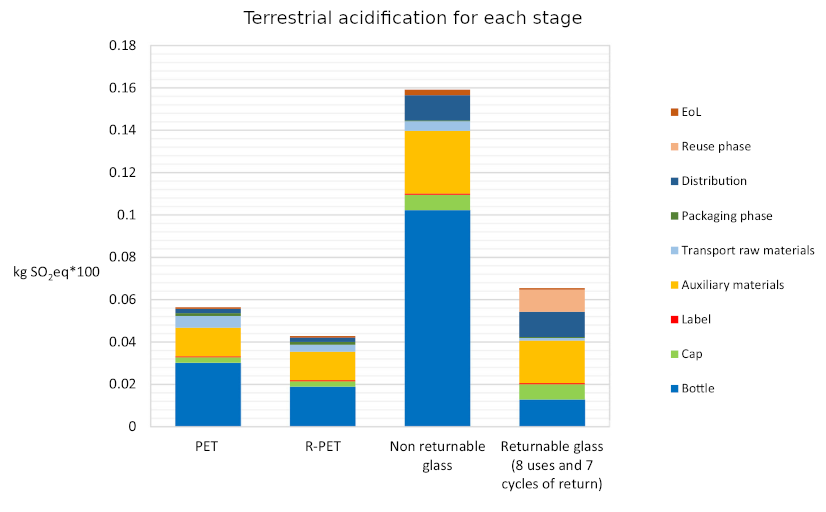
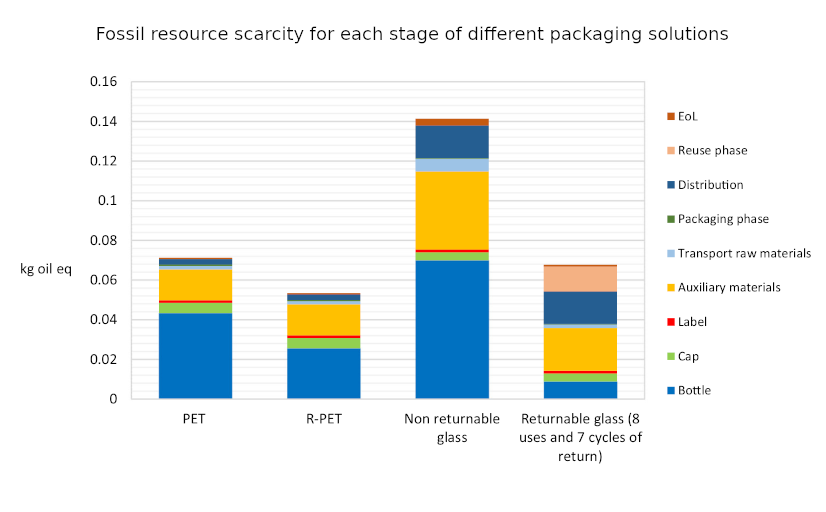
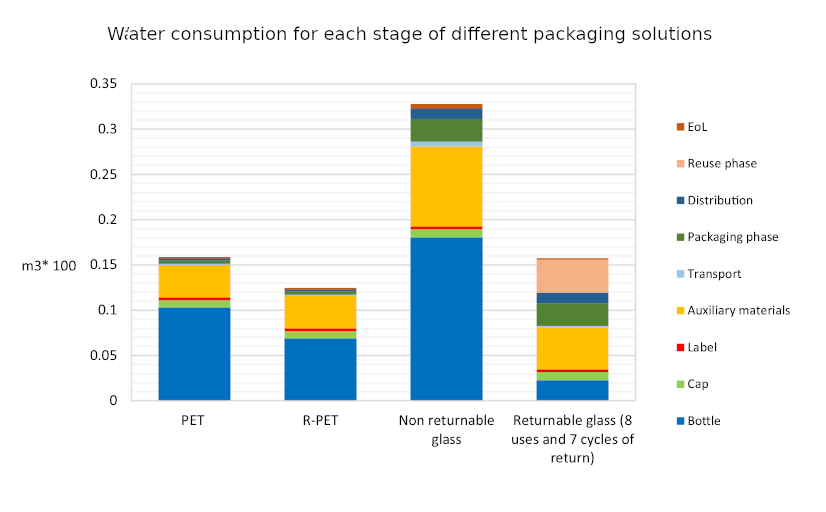
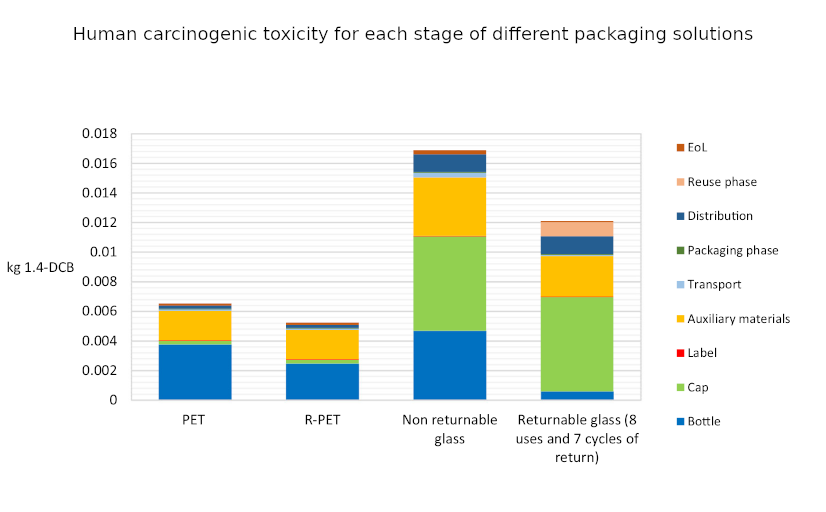


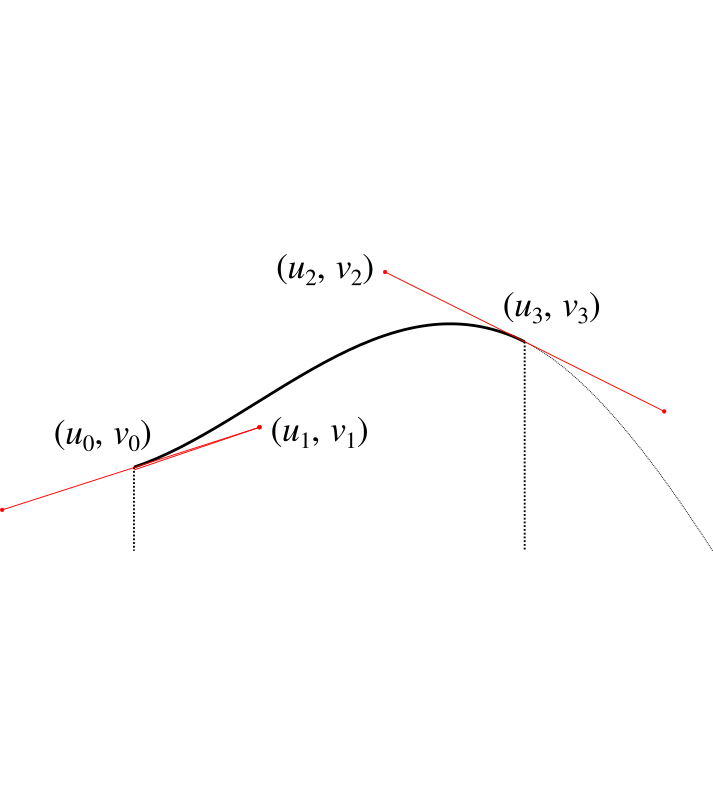
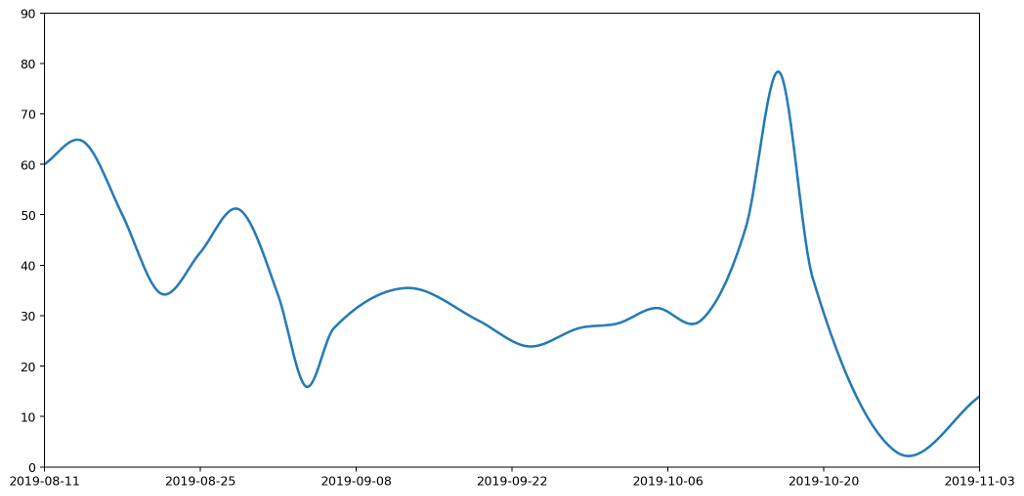
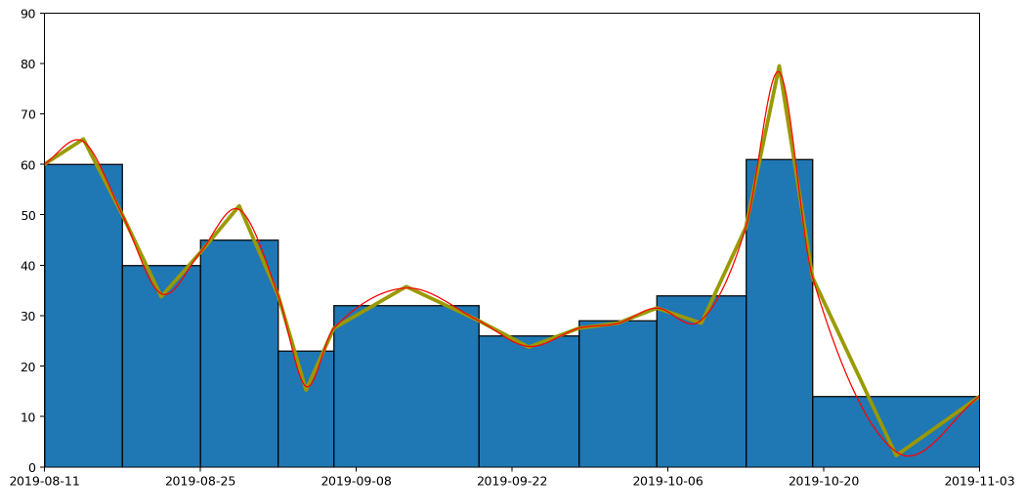
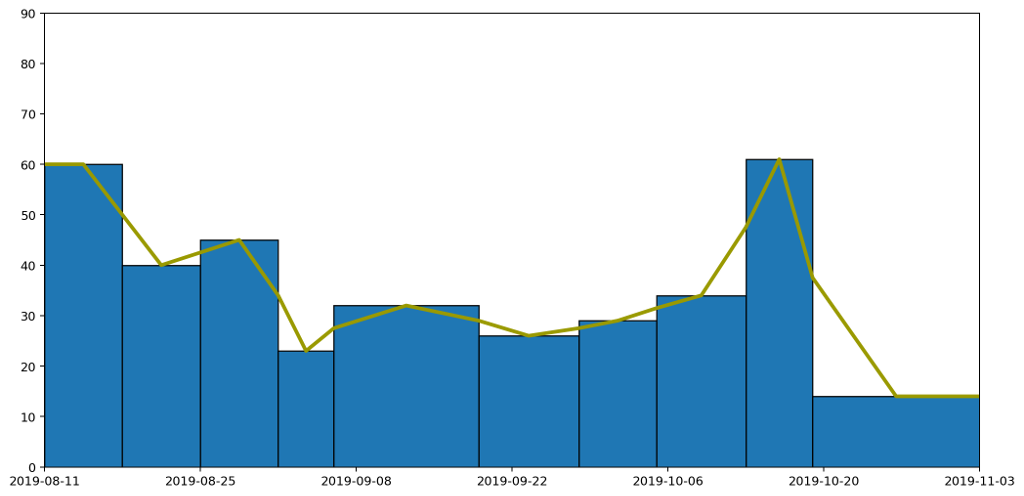



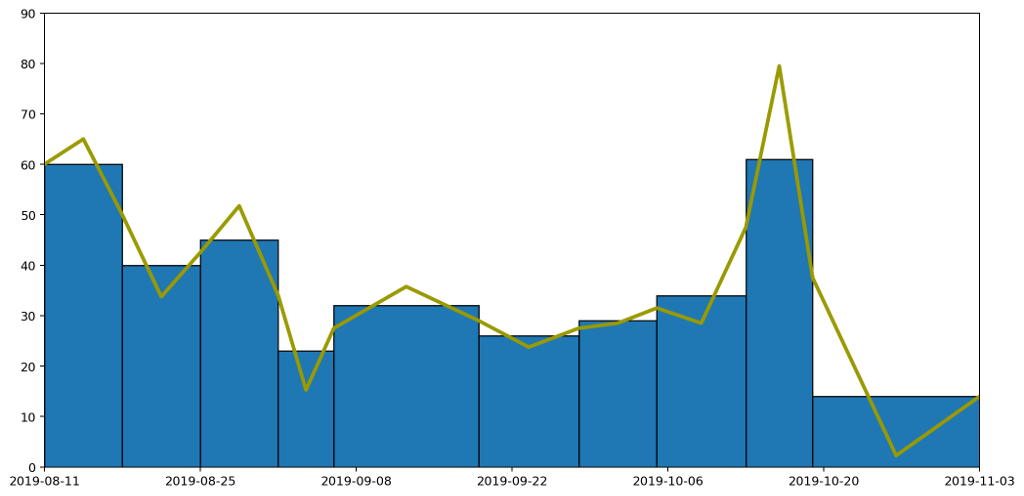
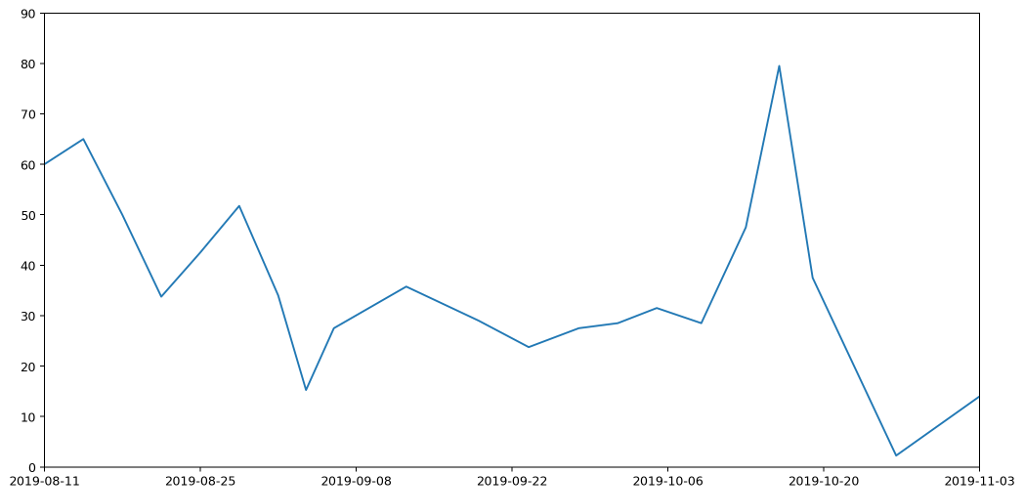

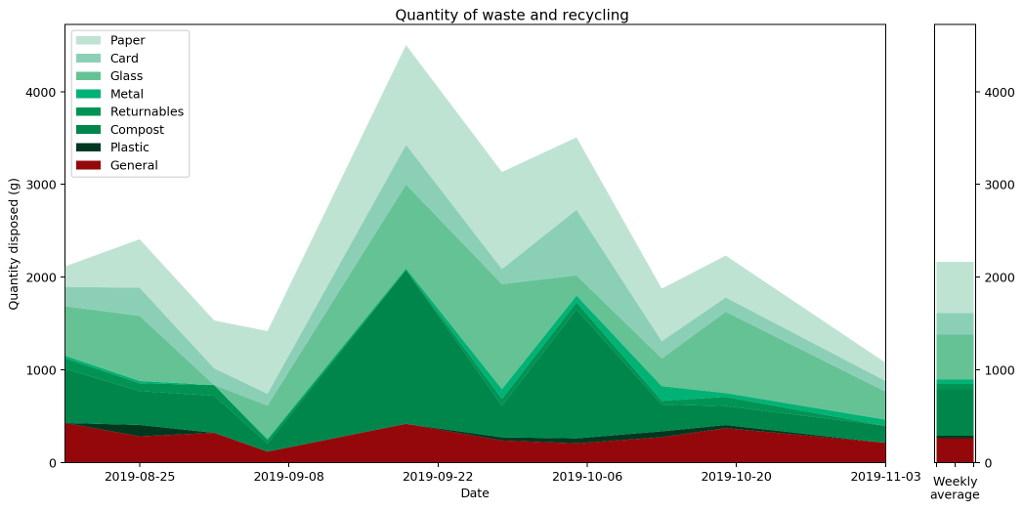
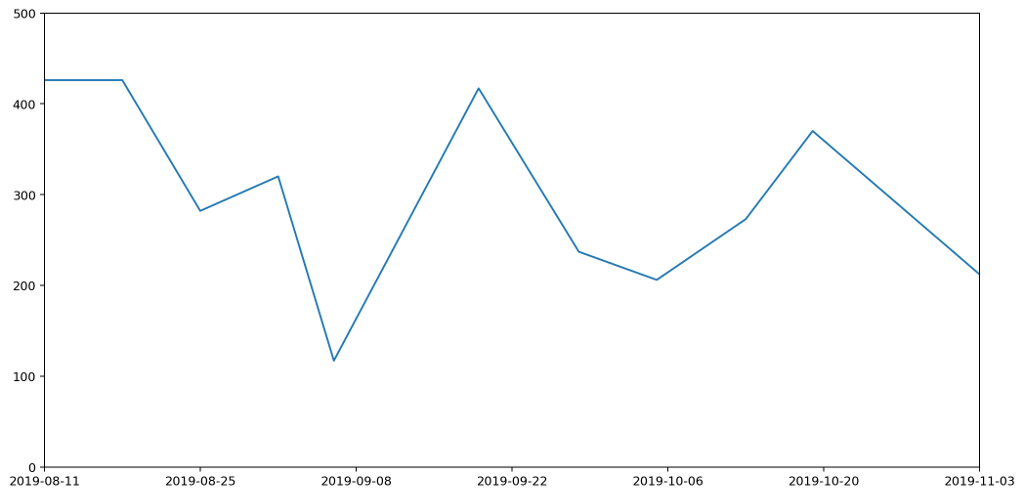
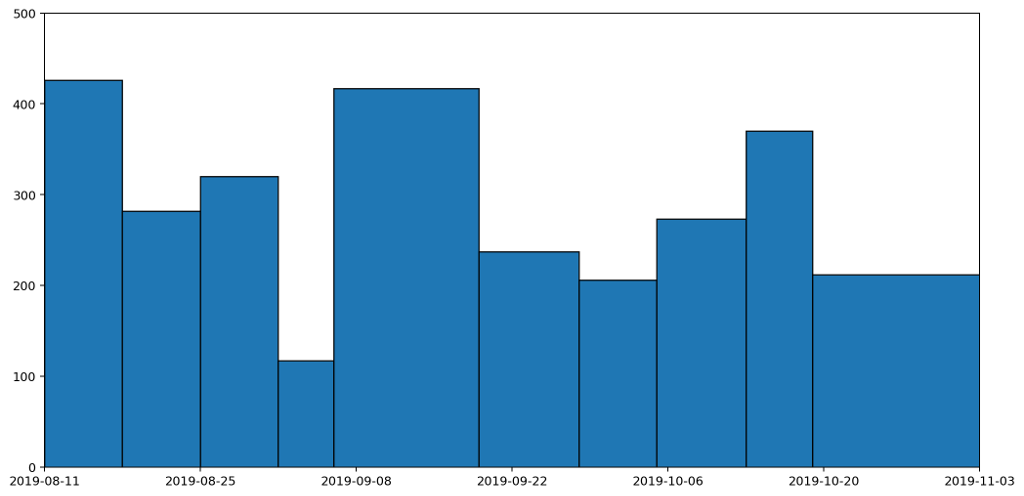
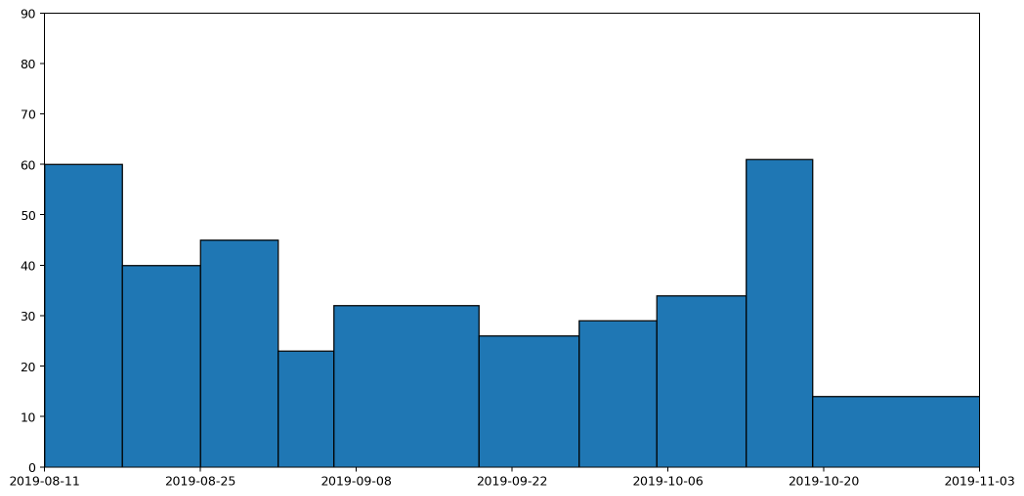
Comments
Uncover Disqus comments