Countable Pseudo-Recursively Saturated Models of Presburger Arithmetic
The following is a brief overview of Presburger arithmetic and pseudo-recursive saturation, which form the basis of my Ph.D. thesis. You can also read my thesis abstract, or get a copy of my entire thesis from the links at the end of this page. If you are interested in this area of mathematics then please feel free to e-mail me. Any suggestions or information will be gratefully received.
Definition: ![]() is a model of Presburger arithmetic if
is a model of Presburger arithmetic if ![]() is an Abelian group with binary operation +, < a linear order and such that
is an Abelian group with binary operation +, < a linear order and such that
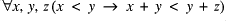 (i.e. order respects
(i.e. order respects  );
); (i.e. order is discrete);
(i.e. order is discrete);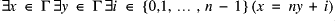 for each
for each 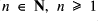 .
.
In A3 we use the following notation:
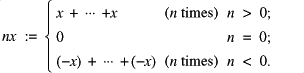
It's also worth pointing out that A3 constitutes an axiom schema rather than a single axiom, which defines the congruence classes of elements mod ![]() . The least positive element described in axiom A2 will also be referred to as 1.
. The least positive element described in axiom A2 will also be referred to as 1.
From A3 we can define the residue map,
![]()
i.e. ![]() .
.
Presburger arithmetic constitutes the theory of addition, for example, as we might expect it to hold in the integers Z.
It is straightforward to show (using our element ![]() and A1) that any model of Presburger arithmetic will have a copy of Z embedded in it. It's therefore possible to consider the quotient group
and A1) that any model of Presburger arithmetic will have a copy of Z embedded in it. It's therefore possible to consider the quotient group
![]()
of a model of Presburger arithmetic, which by A3 will be divisible. An automorphism of ![]() can always be lifted to an automorphism of
can always be lifted to an automorphism of ![]() . Combine this with the divisibility of
. Combine this with the divisibility of ![]() and we discover that the construction of automorphisms becomes considerably easier.
and we discover that the construction of automorphisms becomes considerably easier.
![]()
A representation of a model of Presburger arithmetic ![]()
The notion of a pseudo-recursively saturated model of Presburger arithmetic was developed by Richard Kaye using ideas from a paper by Victor Harnik[1]. No explicit definition of the notion has yet been published. In order to provide a definition here, we first need some other concepts.
Definition: Define
![]()
and consider this as a Dedikind cut identified with some extended real ![]() .
.
If ![]() then
then
![]()
so we can extend this definition to cover the quotient group. i.e. if ![]() then
then
![]()
is well defined and equal to
![]()
Although these 'standard parts' are not actually fractions, they share many of the properties of fractions and with care can often be manipulated in similar ways. For a model ![]() we refer to the set of all such standard parts for the model as
we refer to the set of all such standard parts for the model as ![]() .
.
Definition: ![]() is strongly independent if
is strongly independent if ![]() and
and
![]()
is linearly independent over ![]() as a subset of
as a subset of ![]() for all
for all ![]() .
.
Definition: Suppose ![]() . Let
. Let
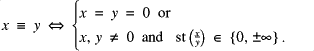
Then ![]() with the set of 'values'
with the set of 'values' ![]() ordered by
ordered by
![]()
We use these definitions of standard parts and values to provide a definition for what we mean by pseudo-recursive saturation.
Definition: If ![]() is a countable model of Presburger arithmetic with
is a countable model of Presburger arithmetic with ![]() then we say that
then we say that ![]() is pseudo-recursively saturated if
is pseudo-recursively saturated if
- for
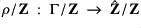 , each
, each 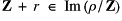 has dense pre-image;
has dense pre-image; - for
 with
with 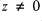 , there is some
, there is some 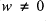 such that
such that
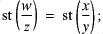
- the set of values
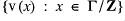 is a dense linear order with respect to < having least point 0 and no greatest point.
is a dense linear order with respect to < having least point 0 and no greatest point.
Pseudo-recursive saturation is designed to capture the properties of a models of Presburger arithmetic which allow automorphisms to be created relatively easily. Normally we might consider models which were recursively saturated, however in the Presburger case this condition is too strong, and for this reason we prefer the weaker condition of pseudo-recursive saturation. It is straightforward to show that ![]() , whilst the reverse direction is not the case. PRS is not, however, any form of saturation in the model theoretic sense.
, whilst the reverse direction is not the case. PRS is not, however, any form of saturation in the model theoretic sense.
The following result gives an indication of why PRS is useful.
Theorem: Suppose ![]() is countable PRS and that
is countable PRS and that
![]()
are strongly independent subsets of ![]() which satisfy the following:
which satisfy the following:
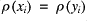 for all
for all 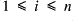 ;
;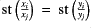 for all
for all  .
.
Then there exists an automorphism ![]() such that
such that ![]() for all
for all ![]() .
.
Because ![]() is taken to be countable, a proof of this can be found by a back-and-forth construction. The PRS models of Presburger arithmetic are also closely connected to homogeneous models and the above result can be used to show one aspect of this connection.
is taken to be countable, a proof of this can be found by a back-and-forth construction. The PRS models of Presburger arithmetic are also closely connected to homogeneous models and the above result can be used to show one aspect of this connection.
The main project of my Ph.D. was to discover all of the closed normal subgroups of the automorphism group of the models described above. It turns out that this can be done using the notion of stQ-closure.
Definition: If ![]() then
then ![]() is stQ-closed if:
is stQ-closed if:
- each
 is non-empty and closed under pointwise multiplication;
is non-empty and closed under pointwise multiplication; - each
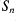 is closed under inversion (where
is closed under inversion (where  );
); - when
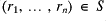 and
and 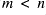 then
then 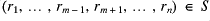 ;
; - when
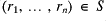 and
and  then there exists at least one
then there exists at least one 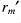 so that
so that 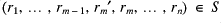 .
.
We find that for a countable PRS model of Presburger arithmetic with trivial centre, the proper non-trivial closed normal subgroups of the automorphism group of ![]() are precisely the sets
are precisely the sets ![]() where
where ![]() is stQ-closed and
is stQ-closed and
![]()
In the above expression we have written maps on the right and ![]() refers to the set of automorphisms which preserve values, that is, the set of all automorphisms
refers to the set of automorphisms which preserve values, that is, the set of all automorphisms ![]() such that
such that ![]() for all
for all ![]() . The only two closed normal subgroups which cannot be written in the above form are therefore the whole automorphism group and also the trivial group containing only the identity map. All other closed normal subgroups, however, can be written as some
. The only two closed normal subgroups which cannot be written in the above form are therefore the whole automorphism group and also the trivial group containing only the identity map. All other closed normal subgroups, however, can be written as some ![]() and all such
and all such ![]() constitute closed normal subgoups.
constitute closed normal subgoups.
Having found all such closed normal subgroups we may be able to discover more properties of the automorphism group, and since automorphisms preserve properties of the Presburger model this may then shed new light on essential properties of Presburger arithmetic. One obvious result which follows from the description of the closed normal subgroups given above is that there are precisely ![]() closed normal subgroups of the automorphism group for a model of Presburger arithmetic as described above.
closed normal subgroups of the automorphism group for a model of Presburger arithmetic as described above.
If you would like to dowload a complete copy of my Ph.D. thesis, please click on one of the links:
- ZIP archive containing thesis in Postscript format (723k);
- Thesis in PDF format (895k);
- ZIP archive containing thesis in DVI format (511k).
Or just the abstract
- ZIP archive containing abstract in Postscript format (282k);
- Abstract in PDF format (22k);
- Abstract in DVI format (4k);
- View the abstract as HTML.
You can also download a poster 'A Galois Correspondence for Z-Groups' which gives a survey of my research into Presburger arithmetic. I first exhibited this at the LMS regional meeting, held in Birmingham University in February 2001:
Finally, if those haven't yet put you off, download the slides for a talk I gave in Oxford, also in February 2002, entitled 'Automorphisms of Models of Presburger Arithmetic':
[1] ![]() -like Recursively Saturated Models of Presburger Arithmetic; Journal of Symbolic Logic, Volume 51, Number 2, June 1996.
-like Recursively Saturated Models of Presburger Arithmetic; Journal of Symbolic Logic, Volume 51, Number 2, June 1996.